Câu hỏi:

08/02/2023 2,410

Trong không gian , cho mặt phẳng và hai điểm , . Gọi sao cho và góc có số đo lớn nhất. Khi đó đẳng thức nào sau đây đúng?

c > 0

a + 2 b = - 6

a + b = 0

a + b = \frac{23}{5}

Xem lời giải

Câu hỏi trong đề: Bộ 15 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn D

Vì

M A = M B

nên M thuộc mặt phẳng trung trực (Q) của đoạn thẳng AB.
Ta có (Q) đi qua trung điểm

I (3; 1; - 1)

của AB và có véctơ pháp tuyến là

\vec{A B} = (2; 4; - 2)

nên (Q) có phương trình là

2 (x - 3) + 4 (y - 1) - 2 (z + 1) = 0 \Leftrightarrow x + 2 y - z - 6 = 0.

Vì

M \in (P)

và

M \in (Q)

nên M thuộc giao tuyến

∆

của (P) và (Q).
(P) có véctơ pháp tuyến

{\vec{n}}_{(P)} = (0; 0; 1)

, (Q) có véctơ pháp tuyến

{\vec{n}}_{(Q)} = (1; 2; - 1)

. Khi đó

∆

có véctơ chỉ phương

\vec{u} = [{\vec{n}}_{(P)}, {\vec{n}}_{(Q)}] = (- 2; 1; 0)

.
Chọn

N (2; 2; 0)

là một điểm chung của (P) và (Q).

Δ

đi qua N nên có phương trình

\{\begin{cases} x = 2 - 2 t \\ y = 2 + t \\ z = 0 \end{cases} (t \in ℝ)

.
Vì

M \in Δ

nên

M = (2 - 2 t; 2 + t; 0)

. Theo định lý cosin trong tam giác MAB, ta có

\cos \hat{A M B} = \frac{M A^{2} + M B^{2} - A B^{2}}{2 M A \cdot M B} = \frac{2 M A^{2} - A B^{2}}{2 M A^{2}} = 1 - \frac{A B^{2}}{2 M A^{2}} .

Vì AB không đổi nên từ biểu thức trên ta có

\hat{A M B}

lớn nhất

\Leftrightarrow \cos \hat{A M B}

nhỏ nhất nhỏ nhất

\Leftrightarrow M A^{2}

.
Ta có

M A^{2} = {(2 t)}^{2} + {(t + 3)}^{2} = 5 t^{2} + 6 t + 9 = 5 {(t + \frac{3}{5})}^{2} + \frac{36}{5} \geq \frac{36}{5}

Đẳng thức xảy ra

\Leftrightarrow t = - \frac{3}{5}

, khi đó

M (\frac{16}{5}; \frac{7}{5}; 0)

.
Vậy

a + b = \frac{23}{5}

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Thể tích khối cầu ngoại tiếp tứ diện đều ABCD cạnh a là

V = \frac{π a^{3} \sqrt{6}}{8}

V = \frac{π a^{3} \sqrt{6}}{4}

V = \frac{π a^{3} \sqrt{3}}{8}

V = \frac{π a^{2} \sqrt{6}}{8}

Lời giải

Chọn A

Gọi H là tâm đường tròn ngoại tiếp

Δ A B C

.
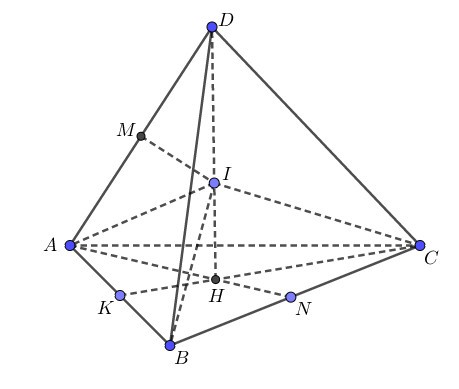
Vì ABCD là tứ diện đều nên DH là trục của đường tròn ngoại tiếp

Δ A B C

.
Mặt phẳng trung trực của cạnh AD cắt DH tại I suy ra ID là bán kính của mặt cầu ngoại tiếp tứ diện ABCD.
Gọi M là trung điểm cạnh AD ta có

Δ D M I ∽ Δ D H A

\Rightarrow \frac{D M}{D H} = \frac{D I}{D A}

\Rightarrow I D = \frac{D A^{2}}{2 D H} = \frac{A D^{2}}{2. \sqrt{A D^{2} - A H^{2}}} = \frac{a^{2}}{2 \sqrt{a^{2} - {(\frac{a}{\sqrt{3}})}^{2}}} = \frac{a \sqrt{6}}{4}

.
Vậy thể tích của khối cầu ngoại tiếp tứ diện ABCD là

V = \frac{4}{3} π . I D^{3} = \frac{4}{3} π . {(\frac{a \sqrt{6}}{4})}^{3} = \frac{π a^{3} \sqrt{6}}{8} .

Câu 2

Trong không gian Oxyz, cho ba điểm $A (0; 1; 2), B (2; - 2; 1)$ , $C (- 2; 1; 0)$ . Khi đó mặt phẳng (ABC) có phương trình là

x + y - z + 1 = 0

6 x + y - z - 6 = 0

x - y + z + 6 = 0

x + y - z - 3 = 0

Lời giải

Chọn A

Ta có

\vec{A B} = (2; - 3; - 1), \vec{A C} = (- 2; 0; - 2)

; Vì

[\vec{A B}, \vec{A C}] = (6; 6; - 6)

nên một vectơ pháp tuyến của (ABC) là

\vec{n} = (1; 1; - 1)

.
Ta có (ABC) qua

A (0; 1; 2)

và nhận

\vec{n} = (1; 1; - 1)

làm vectơ pháp tuyến nên (ABC)có phương trình là

1 (x - 0) + 1 (y - 1) - 1 (z - 2) = 0 \Leftrightarrow x + y - z + 1 = 0

Câu 3

Trong không gian Oxyz, cho hai điểm $A (1; 2; 5), B (3; 0; - 1)$ . Mặt phẳng trung trực của AB đoạn thẳng có phương trình là

x + y - 3 z + 6 = 0

x - y - 3 z + 5 = 0

x - y - 3 z + 1 = 0

2 x + y + 2 z + 10 = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Biết rằng $\int_{0}^{3} \frac{1 - e^{3 x}}{e^{2 x} + e^{x} + 1} d x = a - e^{b}$ với $a, b \in ℤ$ , hãy tính $b - a$ .

b - a = 1

b - a = - 1

b - a = 7

b - a = - 7

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Một quần thể virut Corona P đang thay đổi với tốc độ $P^{'} (t) = \frac{5000}{1 + 0, 2 t}$ , trong đó t là thời gian tính bằng giờ. Quần thể virut Corona P ban đầu (khi $t = 0$ ) có số lượng là 1000 con. Số lượng virut Corona sau 3 giờ gần với số nào sau đây nhất?

A. 16000.

B. 21750.

C. 12750.

D. 11750.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Họ tất cả các nguyên hàm của hàm số $f (x) = 2 \cos x - \sin x$ là

2 \sin x - \cos x + C

- 2 \sin x - \cos x + C

2 \sin x + \cos x + C

- 2 \sin x + \cos x + C

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian Oxyz, cho bốn điểm $A (1; 0; 0)$ , $B (0; 2; 0)$ , $C (0; 0; 4)$ , $M (0; 0; 3)$ . Tính khoảng cách từ M đến mặt phẳng (ABC).

\frac{4 \sqrt{21}}{21}

\frac{2}{21}

\frac{1}{21}

\frac{3 \sqrt{21}}{21}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Trong không gian , cho mặt phẳng và hai điểm , . Gọi sao cho và góc có số đo lớn nhất. Khi đó đẳng thức nào sau đây đúng?

Thể tích khối cầu ngoại tiếp tứ diện đều ABCD cạnh a là

Trong không gian Oxyz, cho ba điểm A0 ; 1 ; 2,B2 ; − 2 ; 1, C− 2 ; 1 ; 0. Khi đó mặt phẳng (ABC) có phương trình là

Trong không gian Oxyz, cho hai điểm A(1 ;2 ;5),B(3 ;0 ; −1). Mặt phẳng trung trực của AB đoạn thẳng có phương trình là

Biết rằng ∫031−e3xe2x+ex+1 dx=a−eb với a, b∈ℤ, hãy tính b−a.

Một quần thể virut Corona P đang thay đổi với tốc độ P't=50001+0,2t, trong đó t là thời gian tính bằng giờ. Quần thể virut Corona P ban đầu (khi t=0) có số lượng là 1000 con. Số lượng virut Corona sau 3 giờ gần với số nào sau đây nhất?

Họ tất cả các nguyên hàm của hàm số fx=2cosx−sinx là

Trong không gian Oxyz, cho bốn điểm A1;0;0, B0;2;0, C0;0;4, M0; 0; 3. Tính khoảng cách từ M đến mặt phẳng (ABC).

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Trong không gian Oxyz, cho ba điểm $A (0; 1; 2), B (2; - 2; 1)$ , $C (- 2; 1; 0)$ . Khi đó mặt phẳng (ABC) có phương trình là

Trong không gian Oxyz, cho hai điểm $A (1; 2; 5), B (3; 0; - 1)$ . Mặt phẳng trung trực của AB đoạn thẳng có phương trình là

Biết rằng $\int_{0}^{3} \frac{1 - e^{3 x}}{e^{2 x} + e^{x} + 1} d x = a - e^{b}$ với $a, b \in ℤ$ , hãy tính $b - a$ .

Họ tất cả các nguyên hàm của hàm số $f (x) = 2 \cos x - \sin x$ là

Trong không gian Oxyz, cho bốn điểm $A (1; 0; 0)$ , $B (0; 2; 0)$ , $C (0; 0; 4)$ , $M (0; 0; 3)$ . Tính khoảng cách từ M đến mặt phẳng (ABC).