Câu hỏi:

10/02/2023 2,860

Người ta muốn sơn một bức tường được tạo thành từ 20 bức tường nhỏ có số đo và hình dạng như hình vẽ bên dưới. Biết mỗi lít sơn được $5 m^{2}$ tường và phần tường phía trên là phần trong của Parabol. Lượng sơn cần dùng gần với giá trị nào dưới đây

A. 16,12.

B. 16,9.

C. 11,12.

D. 12,16.

Xem lời giải

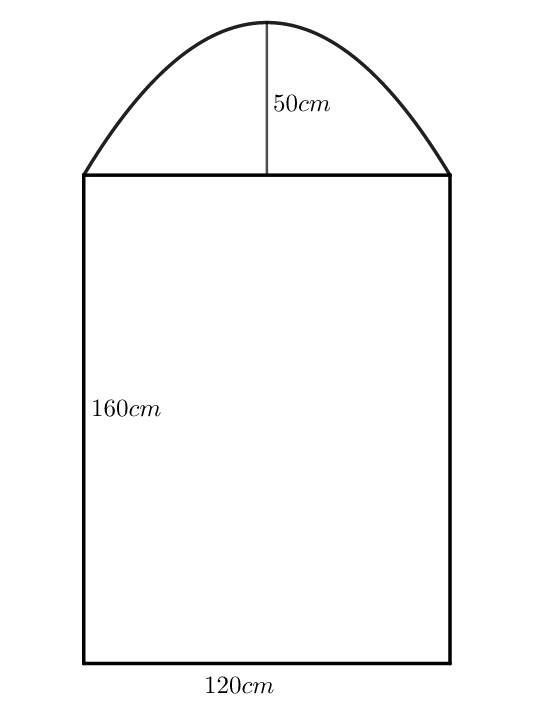
Câu hỏi trong đề: Bộ 15 đề thi giữa kì 2 Toán 12 có đáp án năm 2022-2023 !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Chọn D

Bức trường con gồm hai phần, một phần là hình chữ nhật có diện tích là

S_{1} = 1, 6. (1, 2) = 1, 92 m^{2}

Phần phía trên là phần trong của một Parabol, nên ta sẽ gắn hệ trục tọa độ như sau:
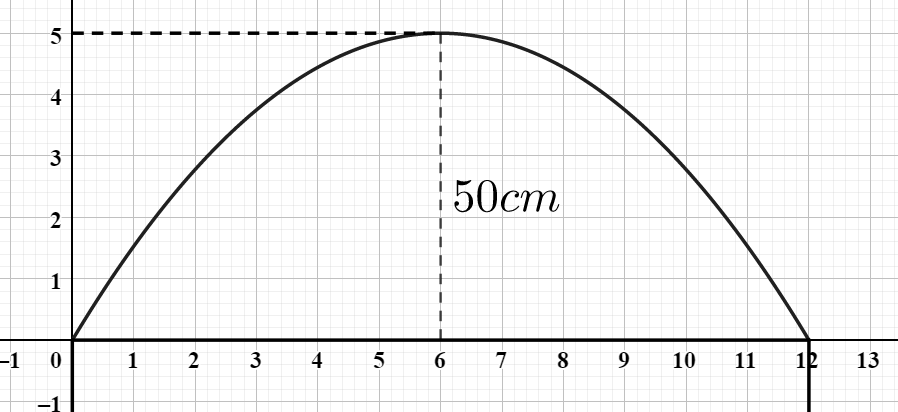
Media VietJack

Từ đó ta có phương trình đường cong là:

y = \frac{- 5}{36} x^{2} + \frac{5}{3} x

.
Áp dụng công thức tính diện tích hình phẳng ta có:

S_{2} = \int_{0}^{1, 2} (\frac{- 5}{36} x^{2} + \frac{5}{3} x) d x = {(\frac{- 5}{108} x^{3} + \frac{5}{6} x^{2})|}_{0}^{1, 2} = 1, 12 m^{2}

Suy ra diện tích 1 bức tường con là:

S = S_{1} + S_{2} = 3, 04 m^{2}

.
Suy ra diện tích cả bức tường to là:

S_{t p} = 20. (3, 04) = 60, 8 m^{2}

Suy ra thể tích sơn cần dùng là:

V = \frac{S_{t p}}{5} = 12, 16 l

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Số tiệm cận đứng của đồ thị hàm số $y = \frac{\sqrt{x + 4} - 2}{x^{2} + x}$ là

A. 3.

B. 0.

C. 2.

D. 1.

Lời giải

Chọn D

Tập xác định:

D = [- 4; + \infty) \ \{- 1; 0\}

.
Tại x = 0, ta có:

\lim_{x \to 0^{+}} \frac{\sqrt{x + 4} - 2}{x^{2} + x} = \lim_{x \to 0^{+}} \frac{x}{x (x + 1) (\sqrt{x + 4} + 2)} = \lim_{x \to 0^{+}} \frac{1}{(x + 1) (\sqrt{x + 4} + 2)} = \frac{1}{4}

và

\lim_{x \to 0^{-}} \frac{\sqrt{x + 4} - 2}{x^{2} + x} = \lim_{x \to 0^{-}} \frac{x}{x (x + 1) (\sqrt{x + 4} + 2)} = \lim_{x \to 0^{-}} \frac{1}{(x + 1) (\sqrt{x + 4} + 2)} = \frac{1}{4}

.
Suy ra x = 0 không phải là đường tiệm cận đứng của đồ thị hàm số.
Tại

x = - 1

, ta có:

\lim_{x \to {(- 1)}^{+}} \frac{\sqrt{x + 4} - 2}{x^{2} + x} = + \infty

(hoặc

\lim_{x \to {(- 1)}^{-}} \frac{\sqrt{x + 4} - 2}{x^{2} + x} = - \infty

).
Suy ra đường thẳng

x = - 1

là tiệm cận đứng của đồ thị hàm số.

Câu 2

Số nghiệm của phương trình $\log_{2} (x^{2} - 3) = \log_{2} 2 x$ là

A. 2.

B. 0.

C. 3.

D. 1.

Lời giải

Chọn D

Ta có

\log_{2} (x^{2} - 3) = \log_{2} 2 x \Leftrightarrow \{\begin{cases} x^{2} - 3 = 2 x \\ x > 0 \end{cases} \Leftrightarrow x = 3

Câu 3

Họ nguyên hàm của hàm số $f (x) = e^{2 x + 3}$ là

\frac{1}{2} e^{2 x + 3} + C

\frac{2}{3} e^{2 x + 3} + C

\frac{3}{2} e^{2 x + 3} + C

\frac{1}{3} e^{2 x + 3} + C

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho khối lăng trụ đứng ABCA'B'C', đáy ABC là tam giác đều cạnh 2a, mặt phẳng (A'BC) tạo với mặt đáy (ABC) góc $60^{o}$ . Tính thể tích khối lăng trụ

V = 3 a^{3}

V = 3 a^{3} \sqrt{3}

V = a^{3} \sqrt{3}

V = a^{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Trong không gian Oxyz, cho hai điểm $A (1; 2; 3)$ , $B (- 1; 4; 1)$ . Phương trình mặt cầu có đường kính là

{(x + 1)}^{2} + {(y - 4)}^{2} + {(z - 1)}^{2} = 12

{(x - 1)}^{2} + {(y - 2)}^{2} + {(z - 3)}^{2} = 12

x^{2} + {(y - 3)}^{2} + {(z - 2)}^{2} = 3

x^{2} + {(y - 3)}^{2} + {(z - 2)}^{2} = 12

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 6 y - 4 = 0$ . Xác định tọa độ tâm I và tính bán kính R của mặt cầu (S).

I (1; - 3; 0), R = \sqrt{14}

I (- 1; 3; 0), R = \sqrt{14}

I (1; - 3; 0), R = \sqrt{10}

I (- 1; 3; 0), R = \sqrt{10}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho $\log_{6} 45 = a + \frac{\log_{2} 5 + b}{\log_{2} 3 + c}$ với a, b, c là các số nguyên. Giá trị bằng $a + b + c$

A. 3.

B. 2.

C. 0.

D. 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Bình luận

Số tiệm cận đứng của đồ thị hàm số y=x+4−2x2+x là

Số nghiệm của phương trình log2x2−3=log22x là

Họ nguyên hàm của hàm số fx=e2x+3 là

Cho khối lăng trụ đứng ABCA'B'C', đáy ABC là tam giác đều cạnh 2a, mặt phẳng (A'BC) tạo với mặt đáy (ABC) góc 60o. Tính thể tích khối lăng trụ

Trong không gian Oxyz, cho hai điểm A1; 2; 3, B−1; 4; 1. Phương trình mặt cầu có đường kính là

Trong không gian Oxyz, cho mặt cầu S: x2+y2+z2−2x+6y−4=0. Xác định tọa độ tâm I và tính bán kính R của mặt cầu (S).

Cho log645=a+log25+blog23+c với a, b, c là các số nguyên. Giá trị bằng a+b+c

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Số tiệm cận đứng của đồ thị hàm số $y = \frac{\sqrt{x + 4} - 2}{x^{2} + x}$ là

Số nghiệm của phương trình $\log_{2} (x^{2} - 3) = \log_{2} 2 x$ là

Họ nguyên hàm của hàm số $f (x) = e^{2 x + 3}$ là

Cho khối lăng trụ đứng ABCA'B'C', đáy ABC là tam giác đều cạnh 2a, mặt phẳng (A'BC) tạo với mặt đáy (ABC) góc $60^{o}$ . Tính thể tích khối lăng trụ

Trong không gian Oxyz, cho hai điểm $A (1; 2; 3)$ , $B (- 1; 4; 1)$ . Phương trình mặt cầu có đường kính là

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 6 y - 4 = 0$ . Xác định tọa độ tâm I và tính bán kính R của mặt cầu (S).

Cho $\log_{6} 45 = a + \frac{\log_{2} 5 + b}{\log_{2} 3 + c}$ với a, b, c là các số nguyên. Giá trị bằng $a + b + c$