Câu hỏi:
16/02/2023 3,760
Cho tứ diện \(ABCD\) có \(AB = 3,AC = 4,AD = 6\), \(\widehat {BAC} = {60^o},\) \(\widehat {CAD} = {90^o},\) \(\widehat {BAD} = {120^o}\). Thể tích của khối tứ diện \(ABCD\) bằng
Câu hỏi trong đề: Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Chọn C
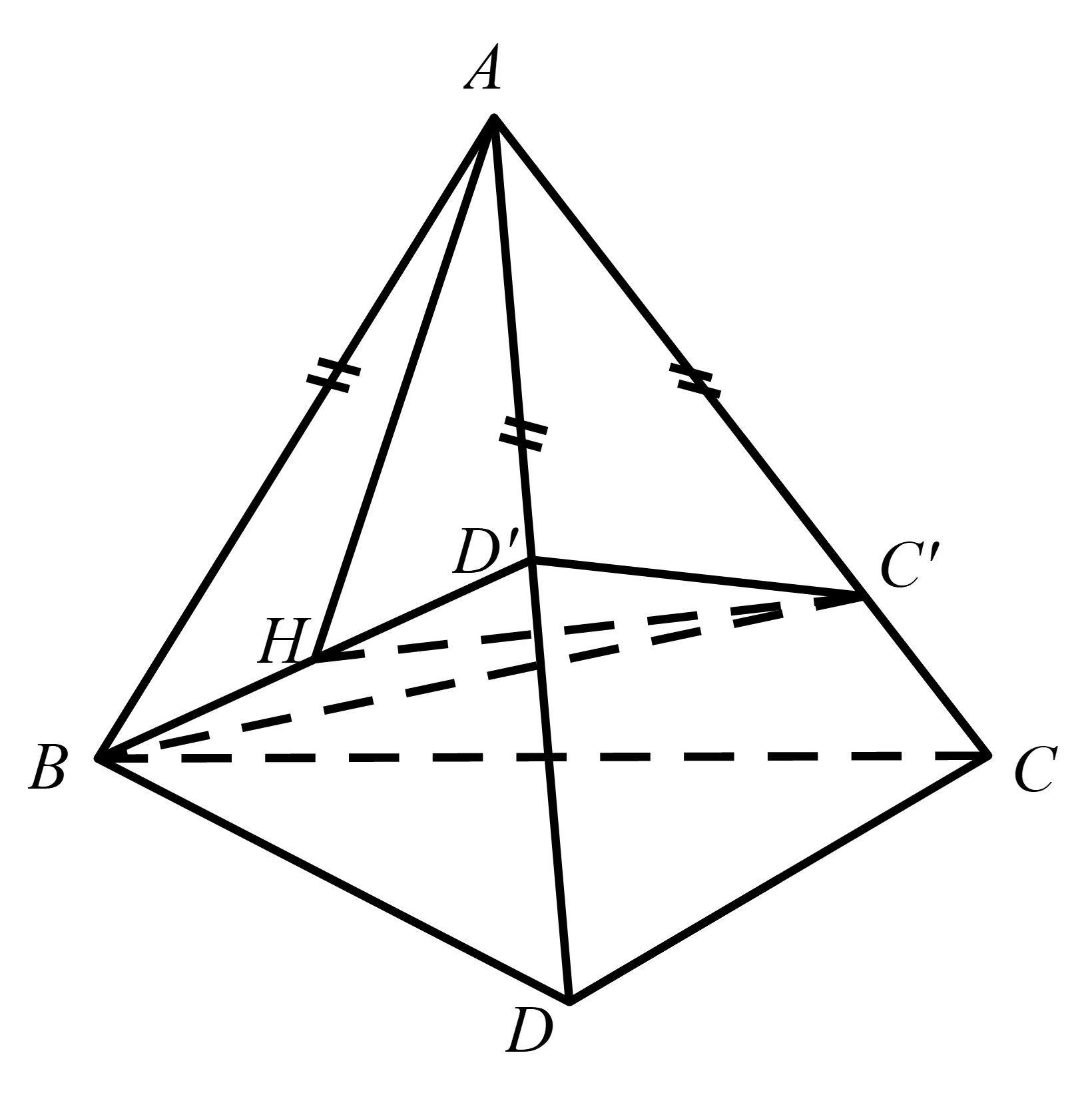
Lấy các điểm \(C',\,\)\(D'\) lần lượt trên cạnh và \(AC,AD\) sao cho \(AB = AC' = AD' = 3\).
Áp dụng định lí Côsin ta có:
\(BD{'^2} = A{B^2} + A{D^{'2}} - 2AB.AD'\cos \widehat {BAD} = 9 + 9 - 2.9.\left( { - \frac{1}{2}} \right) = 9.3 = 27 \Leftrightarrow BD' = 3\sqrt 3 \).
Tam giác \(BAC'\) là tam giác đều nên \(BC' = 3\), tam giác \(D'AC'\) vuông tại \(A\) nên \(C'D' = 3\sqrt 2 \).
Xét tam giác \(BD'C'\) có \(B{D^{'2}} = B{C^{'2}} + C'{D^{'2}}\), nên tam giác vuông tại \(C'\).
Gọi \(H\)là hình chiếu vuông góc của \(A\) trên \(\left( {BD'C'} \right)\), vì \(AB = AC' = AD'\) nên \(HB = HC' = HD'\). Mặt khác, tam giác \(BD'C'\) vuông tại \(C'\) nên \(H\)là trung điểm của \(BD'\).
Ta có, \(AH = \sqrt {A{B^2} - \frac{{B{D^{'2}}}}{4}} = \sqrt {9 - \frac{{27}}{4}} = \frac{3}{2}\).
Thể tích khối tứ diện \(ABC'D'\) bằng
\({V_{ABC'D'}} = \frac{1}{3}AH.{S_{BC'D'}} = \frac{1}{3}.\frac{3}{2}.\frac{1}{2}.3.3\sqrt 2 = \frac{{9\sqrt 2 }}{4}\)
Áp dụng công thức tỉ số thể tích ta có
\(\frac{{{V_{ABC'D'}}}}{{{V_{ABCD}}}} = \frac{{AC'.AD'}}{{AC.AD}} = \frac{3}{4}.\frac{3}{6} = \frac{9}{{24}} \Rightarrow {V_{ABCD}} = \frac{{24}}{9}{V_{ABC'D'}} = 6\sqrt 2 \).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Chọn B
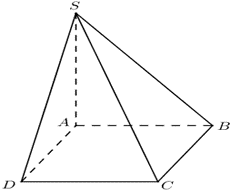
Ta có \[V = \frac{1}{3}SA.{S_{ABCD}} = \frac{1}{3}a\sqrt 2 .{a^2} = \frac{{\sqrt 2 {a^3}}}{3}\].
Lời giải
Lời giải
Chọn D
TXD: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\).
\(y' = 2x - \frac{1}{{{x^2}}}\), \(y' = 0 \Leftrightarrow x = \frac{1}{{\sqrt[3]{2}}}.\)
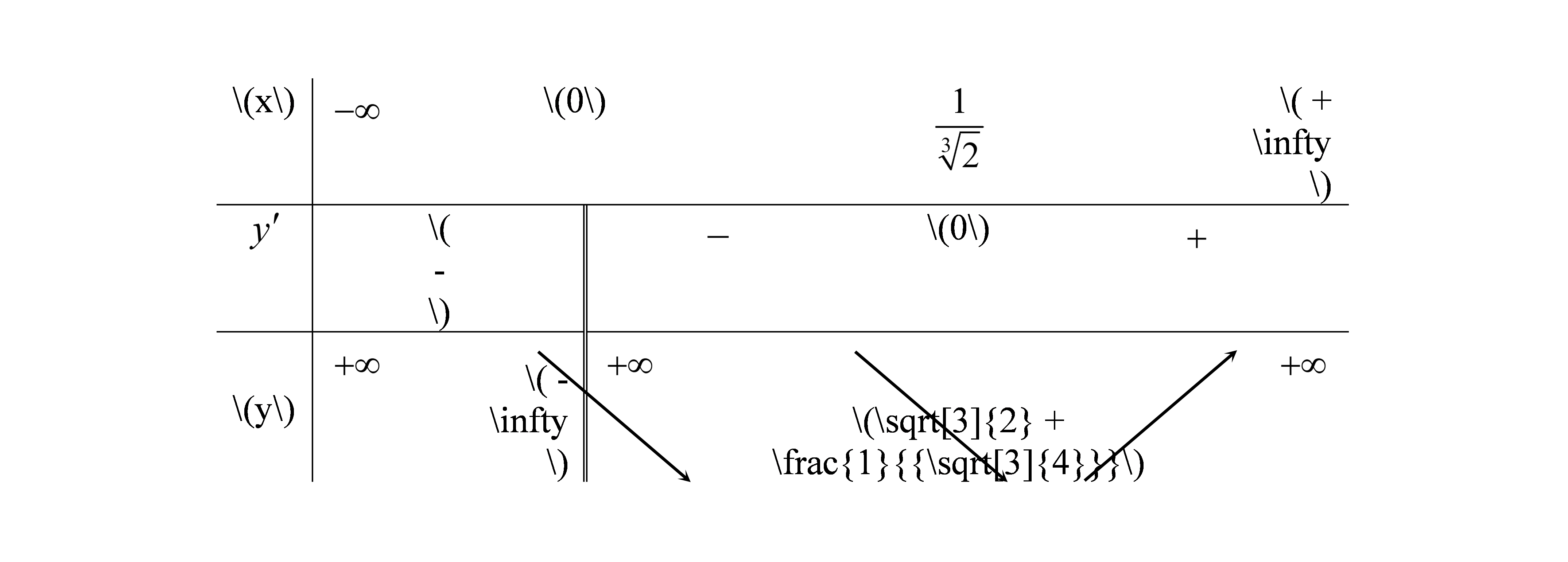
Dựa vào BBT thì \(x = \frac{1}{{\sqrt[3]{2}}}\) hàm số đạt giá trị nhỏ nhất trên \(\left( {0; + \infty } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận