Ông An gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất 7%/năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Sau thời gian 10 năm nếu không rút lần nào thì số tiền mà ông An nhận được tính cả gốc lẫn lãi là (đơn vị đồng):
Ông An gửi số tiền 100 triệu đồng vào ngân hàng với lãi suất 7%/năm, biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi năm số tiền lãi sẽ được nhập vào vốn ban đầu. Sau thời gian 10 năm nếu không rút lần nào thì số tiền mà ông An nhận được tính cả gốc lẫn lãi là (đơn vị đồng):
D. \({10^8}{\left( {1 + 0,7} \right)^{10}}\)
Quảng cáo
Trả lời:
Đáp án B
Phương pháp:
Công thức lãi kép, không kỳ hạn: \({A_n} = M{\left( {1 + r\% } \right)^n}\)
Với: \({A_n}\) là số tiền nhận được sau tháng thứ n, n A
M là số tiền gửi ban đầu,
n là thời gian gửi tiền (tháng),
r là lãi suất định kì (%).
Cách giải:
Số tiền ông An nhận được là: \({A_{10}} = 100\,000\,000.{\left( {1 + 7\% } \right)^{10}} = {10^8}.{\left( {1 + 0,07} \right)^{10}}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án D
Phương pháp:
Đặt \(\cos \,x = t\). Tìm GTLN, GTNN của hàm số với ẩn là t.
Cách giải:
\(y = 2{\sin ^2}x - \cos \,x + 1 = 2 - 2{\cos ^2}x + 1 = - 2{\cos ^2}x - \cos \,x + 3\)Đặt \(\cos \,x = t,\,\,t \in \left[ { - 1;1} \right]\). Hàm số trở thành: \(y = 2{t^2} - t + 3,\,\,\,y' = - 4t - 1 = 0 \Leftrightarrow t = - \frac{1}{4}\)
Ta có: \(y\left( { - 1} \right) = 2,\,\,\,y\left( { - \frac{1}{4}} \right) = \frac{{25}}{8},\,\,\,y\left( 1 \right) = 0\)
\( \Rightarrow \min y = 0 = m,\,\,\,\max y = \frac{{25}}{8} = M \Rightarrow M.m = 0\)
Câu 2
D. \( - 51 \le m \le 19\)
Lời giải
Đáp án A
Tìm miền giá trị của hàm số \(y = {x^3} - 3x - 1\) trên đoạn \(\left[ { - 3;4} \right]\)
Từ đó, xác định giá trị của m để phương trình đã cho có nghiệm trên đoạn \(\left[ { - 3;4} \right]\)
Cách giải:
\({x^3} - 3x + 4m - 1 = 0 \Leftrightarrow {x^3} - 3x - 1 = - 4m\,\,\,\left( * \right)\)
Xét hàm số \(y = {x^3} - 3x - 1\) trên đoạn \(\left[ { - 3;4} \right]\)
Ta có \(y' = 3{x^2} - 3,\,\,\,y' = 0 \Leftrightarrow x = \pm 1\)
Bảng biến thiên:
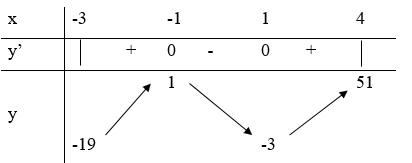
Để phương trình (*) có nghiệm thì \( - 19 \le - 4m \le 51 \Leftrightarrow - \frac{{51}}{4} \le m \le \frac{{19}}{4}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
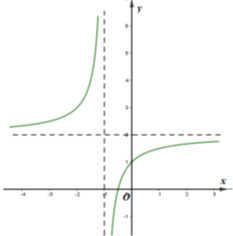
A. \(y = \frac{{2x - 1}}{{x - 1}}\)
C. \(y = \frac{{x + 2}}{{x + 1}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. R
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. \(m = 0\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.