Câu hỏi:
18/02/2023 4,217
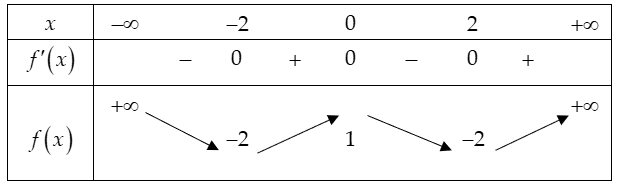
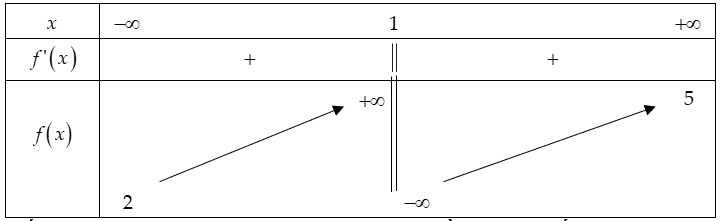
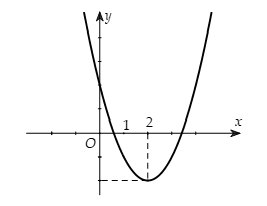
Một đoạn dây thép dài 200(cm) được uốn thành một chiếc khung có dạng như hình vẽ (hai đường cong là hai nữa đường tròn). Khi x thay đổi thì diện tích lớn nhất của hình phẳng thu được gần với giá trị nào sau đây?
Một đoạn dây thép dài 200(cm) được uốn thành một chiếc khung có dạng như hình vẽ (hai đường cong là hai nữa đường tròn). Khi x thay đổi thì diện tích lớn nhất của hình phẳng thu được gần với giá trị nào sau đây?
Đáp án chính xác
Câu hỏi trong đề:
Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án !!
Sách mới 2k7: Tổng ôn Toán, Lí, Hóa, Văn, Sử, Địa…. kỳ thi tốt nghiệp THPT Quốc gia 2025, đánh giá năng lực (chỉ từ 110k).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
Ta có:
Suy ra, diện tích hình phẳng thu được là
Xét hàm số
Xét bảng biến thiên:
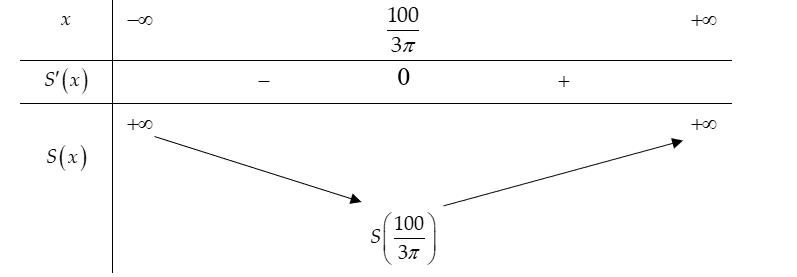
Vậy
Chọn đáp án D.
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Tìm tất cả các giá trị thực của tham số m để hàm số không có cực đại.
Tìm tất cả các giá trị thực của tham số m để hàm số không có cực đại.
Xem đáp án »
18/02/2023
34,995
Câu 2:
Cho hàm số có bảng xét dấu như sau:
Khẳng định nào sau đây đúng?
Cho hàm số có bảng xét dấu như sau:
Khẳng định nào sau đây đúng?
Xem đáp án »
18/02/2023
10,961
Câu 3:
Cho hàm số y=f(x) có bảng biến thiên sau: Số nghiệm của phương trình 2f(x)-3=0 là
Cho hàm số y=f(x) có bảng biến thiên sau: Số nghiệm của phương trình 2f(x)-3=0 là
Xem đáp án »
17/02/2023
10,194
Câu 4:
Cho hàm số có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
Cho hàm số có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
Xem đáp án »
18/02/2023
7,888
Câu 5:
Cho hình chóp có đáy là tam giác vuông tại vuông góc với đáy. Biết SC hợp với một góc thể tích của khối chóp bằng
Cho hình chóp có đáy là tam giác vuông tại vuông góc với đáy. Biết SC hợp với một góc thể tích của khối chóp bằng
Xem đáp án »
18/02/2023
6,074
Câu 6:
Cho hàm số liên tục trên R và có đồ thị như hình bên. Tìm số điểm cực trị hàm số
Cho hàm số liên tục trên R và có đồ thị như hình bên. Tìm số điểm cực trị hàm số
Xem đáp án »
18/02/2023
5,609
Bình luận
🔥 Đề thi HOT:
-
53 câu Bài tập về Tính đơn điệu của hàm số có lời giải (P1)
-
7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án ( Phần 1)
-
200 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao (P1)
-
120 câu Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P1)
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
-
124 câu Trắc nghiệm Ôn tập Toán 12 Chương 3 Hình học có đáp án (Phần 1)
-
250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P1)
về câu hỏi!