Câu hỏi:

17/02/2023 442

Cho hình chóp SABCD có đáy là hình bình hành. Gọi M,N là trung điểm của SA, SB Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần.

Tỉ số thể tích hai phần (số bé chia số lớn) là

A. $\frac{3}{5} .$

B. $\frac{3}{4} .$

C. $\frac{1}{3} .$

D. $\frac{4}{5} .$

Xem lời giải

Câu hỏi trong đề: Bộ 20 đề thi giữa học kì 1 Toán 12 năm 2022-2023 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Lời giải:

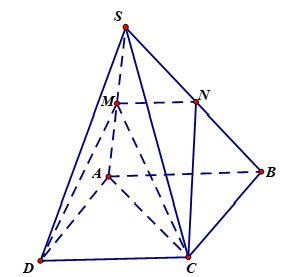
Cho hình chóp SABCD có đáy là hình bình hành. Gọi M,N là trung điểm của SA, SB Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần. (ảnh 1)

Giả sử thể tích của khối chóp là

Ta có $\frac{V_{S . M D C}}{V_{S . A D C}} = \frac{S M}{S A} . \frac{S D}{S D} . \frac{S C}{S C} = \frac{1}{2};$ $\frac{V_{S . M N C}}{V_{S . A B C}} = \frac{S M}{S A} . \frac{S N}{S B} . \frac{S C}{S C} = \frac{1}{4};$

$\frac{V_{S . M D C}}{V_{S . A D C}} + \frac{V_{S . M N C}}{V_{S . A B C}} = \frac{V_{S . M D C}}{\frac{1}{2} V} + \frac{V_{S . M N C}}{\frac{1}{2} V} = \frac{V_{S . M N C D}}{\frac{1}{2} V} = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}$

$\Rightarrow V_{S . M N C D} = \frac{3}{8} V \Rightarrow V_{M N A B C D} = V - \frac{3}{8} V = \frac{5}{8} V \Rightarrow \frac{V_{S . M N C D}}{V_{M N A B C D}} = \frac{3}{5} .$

Chọn đáp án A.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Tìm tất cả các giá trị thực của tham số m để hàm số $y = (m - 1) x^{4} - 2 (m - 3) x^{2} + 1$ không có cực đại.

A. $1 \leq m \leq 3$

B. $m \leq 1$

C. $m \geq 1$

D. $1 < m < 3$

Lời giải

Lời giải:

Ta có $y^{'} = 4 (m - 1) x^{3} - 4 (m - 3) x = 4 x [(m - 1) x^{2} - (m - 3)]$

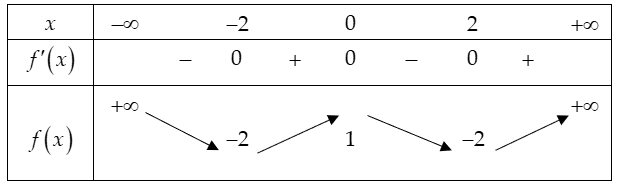
Xét với m=1 : Khi đó $y = 4 x^{2} + 1$ hàm số không có cực đại. Vậy m=1 thỏa mãn (1)

Xét với $m > 1$ : Khi đó hàm số là hàm bậc 4 trùng phương với hệ số $a > 0$ để hàm số không có cực đại thì $y^{'} = 0$ chỉ có một nghiệm duy nhất x=0 .

Hay $(m - 1) x^{2} - (m - 3) = 0$ vô nghiệm hoặc có nghiệm kép x=0 .

$\Leftrightarrow x^{2} = \frac{m - 3}{m - 1}$ vô nghiệm hoặc có nghiệm x=0 $\Leftrightarrow \frac{m - 3}{m - 1} \leq 0 \Leftrightarrow 1 < m \leq 3$ (2)

Xét với $m < 1$ : Hàm số bậc 4 trùng phương có hệ số $a < 0$ luôn có cực đại (3)

Kết luận : Từ (1), (2), (3) ta có để hàm số không có cực đại thì $1 \leq m \leq 3$ .

Chọn đáp án A.

Câu 2

Cho hàm số $y = a x^{3} + b x^{2} + c x + 2, (a; b; c \in ℝ)$ có bảng xét dấu như sau:

Khẳng định nào sau đây đúng?

A. $a > 0; b < 0; c < 0$

B. $a > 0; b < 0; c > 0$

C. $a > 0; b > 0; c < 0$

D. $a > 0; b > 0; c > 0$

Lời giải

Lời giải:

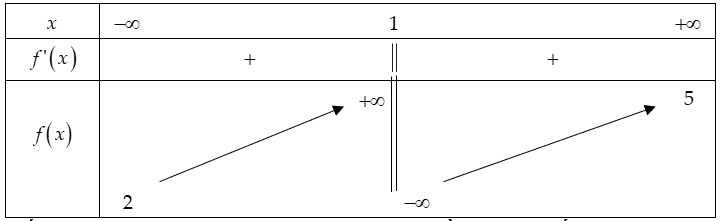
Ta có $y^{'} = 3 a x^{2} + 2 b x + c$ .

Phương trình $y^{'} = 0$ có hai nghiệm $x_{1} < x_{2} < 0$ nên $\{\begin{cases} x_{1} + x_{2} = \frac{- 2 b}{3 a} < 0 (1) \\ x_{1} . x_{2} = \frac{c}{3 a} > 0 (2) \end{cases}$

Từ $(1); (2)$ suy ra $a; b; c$ cùng dấu. Hơn nữa $y^{'} (0) = c > 0$ nên $a > 0; b > 0; c > 0$ .

Chọn đáp án D.

Câu 3

Cho hàm số y=f(x) có bảng biến thiên sau: Số nghiệm của phương trình 2f(x)-3=0 là

A. 4

B. 3

C. 2

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

A. 4

B. 1

C. 3

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Cho hình chóp $S . A B C$ có đáy là tam giác vuông tại $B, A B = a, B C = 2 a, S A$ vuông góc với đáy. Biết SC hợp với $(S A B)$ một góc $30^{0},$ thể tích của khối chóp $S . A B C$ bằng

A. $\frac{\sqrt{15} a^{3}}{3} .$

B. $\frac{\sqrt{5} a^{3}}{2} .$

C. $\frac{\sqrt{11} a^{3}}{3} .$

D. $\frac{\sqrt{3} a^{3}}{3} .$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số $y = f (x)$ liên tục trên R và có đồ thị như hình bên. Tìm số điểm cực trị hàm số $y = f (|x| + 2) .$

A. 2

B. 3

C. 1

D. 5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Giá trị lớn nhất của hàm số $f (x) = x^{3} - 3 x + 2$ trên đoạn $[- 3; 3]$ bằng

A. -16

B. 20

C. 0

D. 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình chóp SABCD có đáy là hình bình hành. Gọi M,N là trung điểm của SA, SB Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần. Tỉ số thể tích hai phần (số bé chia số lớn) là

Tìm tất cả các giá trị thực của tham số m để hàm số y=m−1x4−2m−3x2+1 không có cực đại.

Cho hàm số y=ax3+bx2+cx+2, a; b; c∈ℝ có bảng xét dấu như sau: Khẳng định nào sau đây đúng?

Cho hàm số y=f(x) có bảng biến thiên sau: Số nghiệm của phương trình 2f(x)-3=0 là

Cho hàm số y=fx có bảng biến thiên như sau: Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

Cho hình chóp S.ABC có đáy là tam giác vuông tại B, AB=a, BC=2a, SA vuông góc với đáy. Biết SC hợp với SAB một góc 300, thể tích của khối chóp S.ABC bằng

Cho hàm số y=fx liên tục trên R và có đồ thị như hình bên. Tìm số điểm cực trị hàm số y=fx+2.

Giá trị lớn nhất của hàm số fx=x3−3x+2 trên đoạn −3;3 bằng

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Cho hình chóp SABCD có đáy là hình bình hành. Gọi M,N là trung điểm của SA, SB Mặt phẳng (MNCD) chia hình chóp đã cho thành hai phần.

Tỉ số thể tích hai phần (số bé chia số lớn) là

Tìm tất cả các giá trị thực của tham số m để hàm số $y = (m - 1) x^{4} - 2 (m - 3) x^{2} + 1$ không có cực đại.

Cho hàm số $y = a x^{3} + b x^{2} + c x + 2, (a; b; c \in ℝ)$ có bảng xét dấu như sau:

Khẳng định nào sau đây đúng?

Cho hàm số $y = f (x)$ có bảng biến thiên như sau:

Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

Cho hình chóp $S . A B C$ có đáy là tam giác vuông tại $B, A B = a, B C = 2 a, S A$ vuông góc với đáy. Biết SC hợp với $(S A B)$ một góc $30^{0},$ thể tích của khối chóp $S . A B C$ bằng

Cho hàm số $y = f (x)$ liên tục trên R và có đồ thị như hình bên. Tìm số điểm cực trị hàm số $y = f (|x| + 2) .$

Giá trị lớn nhất của hàm số $f (x) = x^{3} - 3 x + 2$ trên đoạn $[- 3; 3]$ bằng