Tìm số đường tiệm cận của đồ thị hàm số \(y = \frac{{5x + 11}}{{\sqrt {3{x^2} + 2017} }}\)
Tìm số đường tiệm cận của đồ thị hàm số \(y = \frac{{5x + 11}}{{\sqrt {3{x^2} + 2017} }}\)
D. 3
Quảng cáo
Trả lời:
Đáp án C
Phương pháp:
* Định nghĩa tiệm cận ngang của đồ thị hàm số \(y = f\left( x \right)\)
Nếu \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = a\) hoặc \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = a \Rightarrow y = a\)là TCN của đồ thị hàm số.
* Định nghĩa tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\)
Nếu \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = - \infty \) hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = + \infty \) hoặc \(\mathop {\lim }\limits_{x \to {a^ - }} f\left( x \right) = - \infty \) thì \(x = a\) là TCĐ của đồ thị hàm số.
Cách giải:
TXĐ: \(D = R\)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{5x + 11}}{{\sqrt {3{x^2} + 2017} }} = \mathop {\lim }\limits_{x \to + \infty } \frac{{5 + \frac{{11}}{x}}}{{\sqrt {3 + \frac{{2017}}{{{x^2}}}} }} = \frac{5}{{\sqrt 3 }};\,\,\,\,\mathop {\lim }\limits_{x \to - \infty } \frac{{5x + 11}}{{\sqrt {3{x^2} + 2017} }} = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 + \frac{{11}}{x}}}{{ - \sqrt {3 + \frac{{2017}}{{{x^2}}}} }} = - \frac{5}{{\sqrt 3 }}\)
Đồ thị hàm số \(y = \frac{{5x + 1}}{{\sqrt {3{x^2} + 2017} }}\) có 2 đường tiệm cận là \(y = \frac{5}{{\sqrt 3 }},\,\,\,y = - \frac{5}{{\sqrt 3 }}\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
D. \(m \in \left( { - \infty ;3} \right)\)
Lời giải
Đáp án C
Phương pháp:
Biến đổi, đặt \({\log _2}\left( {{5^x} - 1} \right) = t,\,\,t \ge 2\)
Cách giải:
\({\log _2}\left( {{5^x} - 1} \right).{\log _4}\left( {{{2.5}^x}} \right) - 2 = m\)
\( \Leftrightarrow {\log _2}\left( {{5^x} - 1} \right).{\log _{{2^2}}}\left( {{{2.5}^x}} \right) - 1 = m\)
\( \Leftrightarrow \frac{1}{2}{\log _2}\left( {{5^x} - 1} \right).1 + {\log _2}\left( {{5^x} - 1} \right) = m\)
\( \Leftrightarrow \log _2^2\left( {{5^x} - 1} \right) + {\log _2}\left( {{5^x} - 1} \right) - 2m = 0\)
Đặt \({\log _2}\left( {{5^x} - 1} \right) = t,\,\,t \ge 2\), phương trình trở thành: \({t^2} + t = 2m = 0,\,\,t \ge 2 \Leftrightarrow {t^2} + t = 2m,\,\,t \ge 2\left( * \right)\)
Xét hàm số \(f\left( t \right) = {t^2} + t,\,\,t \ge 2\) có: \(f'\left( t \right) = 2t + 1 > 0,\,\,\,\forall t \ge 2 \Rightarrow \) Hàm số đồng biến trên khoảng \(\left[ {2; + \infty } \right)\)
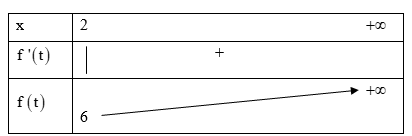
Để phương trình (*) có nghiệm thì \(2m \ge 6 \Leftrightarrow m \ge 3\)
Câu 2
D. \(m \in \left( {1; + \infty } \right)\)
Lời giải
Đáp án A
Phương pháp:
+) Giải phương trình hoành độ giao điểm của hai hàm số, tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.
+) Sử dụng định lí Vi-et.
Cách giải:
Phương trình hoành độ giao điểm của \(y = - mx\) và \(y = {x^3} - 3{x^2} - m + 2\)
\({x^3} - 3{x^2} - m + 2 = - mx \Leftrightarrow {x^3} - 3{x^2} + mx - m + 2 = 0\)
\( \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2x + m - 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} - 2x + m - 2 = 0\left( 2 \right)\end{array} \right.\)
Để đường thẳng \(y = - mx\) cắt đồ thị hàm số \(y = {x^3} - 3{x^2} - m + 2\) tại ba điểm A,B,C phân biệt thì (2) có 2 nghiệm phân biệt và khác 1
\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\1 - 2 + m - 2 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}1 - m + 2 > 0\\m - 3 \ne 0\end{array} \right. \Leftrightarrow m < 3\)
Khi đó, giả sử (2) có 2 nghiệm \({x_1},\,{x_2}\left( {{x_1} < {x_2}} \right)\). Theo Vi ét: \({x_1} + {x_2} = 2\)
Mà \({y_1} = - m{x_1},\,\,{y_2} = - m{x_2} \Rightarrow {y_1} + {y_2} = - m\left( {{x_1} + {x_2}} \right) = - 2m\)
Đặt \(A\left( {{x_1};{y_1}} \right),\,\,B\left( {1; - m} \right),\,\,C\left( {{x_2};{y_2}} \right) \Rightarrow \) B là trung điểm của AC với mọi \(m < 3\)
Câu 3
D. \(m = 3\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
D. \(\frac{5}{4}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
D. \(y = \left| {\ln x} \right|\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
D. \(5\left( {cm} \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.