Cho hình thang cân có độ dài đáy nhỏ và hai cạnh bên đều bằng \(1\) mét. Khi đó hình thang đã cho có diện tích lớn nhất bằng?
Câu hỏi trong đề: Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án !!
Quảng cáo
Trả lời:
Lời giải
Chọn C
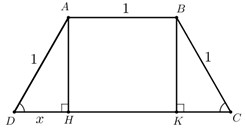
Kẻ \(AH \bot CD,BK \bot CD \Rightarrow ABKH\) là hình chữ nhật \( \Rightarrow AB = HK = 1\left( m \right).\)
Đặt \(DH = x.\) Khi đó \(AH = \sqrt {1 - {x^2}} \left( {0 < x < 1} \right).\)
Vì \(ABCD\) là hình thang cân nên \(\Delta ADH = \Delta BCK\) (cạnh huyền – góc nhọn)
\( \Rightarrow DH = CK = x \Rightarrow CD = DH + HK + CK = 2x + 1.\)
Ta có \({S_{ABCD}} = \frac{{\left( {AB + CD} \right).AH}}{2} = \frac{{\left( {1 + 2x + 1} \right)\sqrt {1 - {x^2}} }}{2} = \left( {x + 1} \right)\sqrt {1 - {x^2}} .\)
Xét hàm số \(f\left( x \right) = \left( {x + 1} \right)\sqrt {1 - {x^2}} \left( {0 < x < 1} \right),\) ta có
\(f'\left( x \right) = \sqrt {1 - {x^2}} - \frac{{2x\left( {x + 1} \right)}}{{2\sqrt {1 - {x^2}} }} = \frac{{ - 2{x^2} - x + 1}}{{\sqrt {1 - {x^2}} }},\) \(f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \frac{1}{2}\left( n \right)}\\{x = - 1\left( l \right)}\end{array}} \right..\)
Bảng biến thiên:
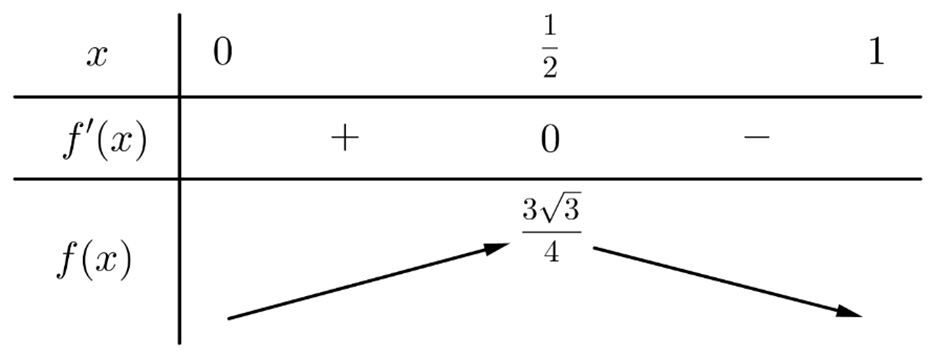
Dựa vào bảng biến thiên, ta thấy \(f\left( x \right) \le f\left( {\frac{1}{2}} \right) = \frac{{3\sqrt 3 }}{4}.\)
Vậy diện tích lớn nhất của hình thang \(ABCD\) là \(\frac{{3\sqrt 3 }}{4}\left( {{m^2}} \right).\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Lời giải
Chọn D
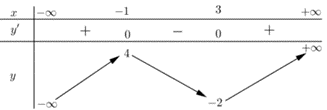
Ta có \[f'\left( x \right) = {\left( {x + 1} \right)^2}{\left( {x - 1} \right)^3}\left( {2 - x} \right) \Rightarrow f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = 2\end{array} \right.\].
Từ đó, ta có bảng biến thiên như sau:
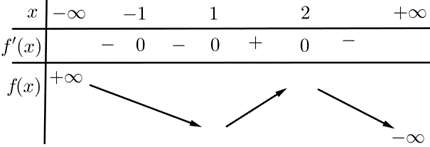
Dựa vào bảng biến thiên thì hàm số \[y = f\left( x \right)\] đồng biến trên \(\left( {1\,;\,2} \right)\).
Câu 2
Lời giải
Lời giải
Chọn D
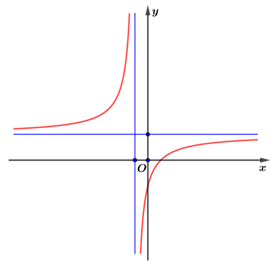
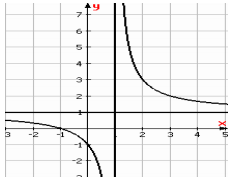
Đồ thị hàm số \[y = \frac{{ax + b}}{{cx + d}}\] đi qua \(M\left( {0\,;\,\frac{b}{d}} \right)\), có đường tiệm cận đứng \(x = - \frac{d}{c}\), đường tiệm cận ngang \(y = \frac{a}{c}\).
Quan sát đồ thị thấy:
+ Giao điểm với trục tung nằm phía dưới \(Ox\)nên \(\frac{b}{d} < 0 \Leftrightarrow bd < 0\)\( \Rightarrow \) Loại phương án
+ Đường tiệm cận ngang nằm phía trên \(Ox\)nên \(\frac{a}{c} > 0 \Leftrightarrow ac > 0\)\( \Rightarrow \) Loại phương án
+ Đường tiệm cận đứng nằm bên trái \(Oy\)nên \( - \frac{d}{c} < 0 \Leftrightarrow cd > 0\).
Ta có: \(\left\{ \begin{array}{l}bd < 0\\cd > 0\end{array} \right. \Rightarrow bc < 0\)\( \Rightarrow \) Loại phương án
Kiểm chứng phương án D: \(\left\{ \begin{array}{l}ac > 0\\cd > 0\end{array} \right. \Rightarrow ad > 0\); \(\left\{ \begin{array}{l}ad > 0\\bd < 0\end{array} \right. \Rightarrow ab < 0\).
Lưu ý: Có thể sử dụng giao điểm của đồ thị với trục hoành nằm bên phải \(Oy\)nên \( - \frac{b}{a} > 0 \Leftrightarrow ab < 0\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.