Câu hỏi:
21/02/2023 1,809
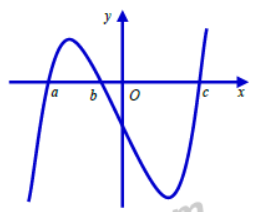
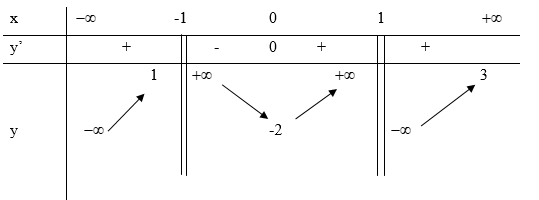
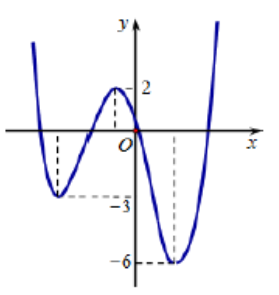
Gọi S là tập hợp các giá trị thực của tham số m để hàm số \(y = {x^3} - 3m{x^2} + 4{m^3}\) có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng
Gọi S là tập hợp các giá trị thực của tham số m để hàm số \(y = {x^3} - 3m{x^2} + 4{m^3}\) có hai điểm cực trị A và B sao cho tam giác OAB có diện tích bằng 4 (là gốc tọa độ). Ta có tổng giá trị tất cả các phần tử của tập S bằng
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án B
Phương pháp:
+) Tìm điều kiện để hàm số có 2 điểm cực trị.
+) Xác định các điểm cực trị của hàm số, nhận xét vị trí các điểm cực trị và tính diện tích tam giác.
Cách giải:
\(y = {x^3} - 3m{x^2} + 4{m^3} \Rightarrow y' = 3{x^2} - 6mx\). Ta có \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2m\end{array} \right.\)
Để hàm số đã cho có hai điểm cực trị thì \(m \ne 0\). Khi đó:
\(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0 \Rightarrow y\left( 0 \right) = 4{m^3} \Rightarrow A\left( {0;4{m^3}} \right) \in Oy\\x = 2m \Rightarrow y\left( {2m} \right) = 0 \Rightarrow B\left( {2m;0} \right) \in Ox\end{array} \right.\)
Vậy tam giác OAB vuông tại O nên \({S_{\Delta OAB}} = \frac{1}{2}OA.OB \Leftrightarrow 4 = \frac{1}{2}\left| {4{m^3}} \right|\left| {2m} \right|\)
\( \Leftrightarrow \left| {{m^4}} \right| = 1 \Leftrightarrow \left[ \begin{array}{l}m = - 1\\m = 1\end{array} \right. \Rightarrow S\left\{ {1; - 1} \right\}\)
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án D
Phương pháp:
Giải bất phương trình \(y' < 0\)
Cách giải:
Tập xác định \(D = R\)
\(y' = {x^3} - 4x + 3;\,\,\,y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\)
Bảng biến thiên:
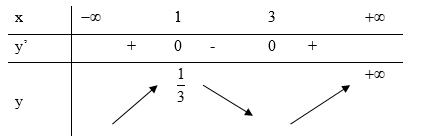
Từ bảng biến thiên, ta thấy hàm số nghịch biến trên \(\left( {1;3} \right)\)
Lời giải
Đáp án C
Phương pháp:
Số điểm cực trị của hàm số \(y = f\left( x \right)\) là số điểm mà qua đó \(f'\left( x \right)\) đổi dấu.
Cách giải:
\(y = f\left( x \right) - 2x \Rightarrow y' = f'\left( x \right) - 2\)
Ta có: \(y' = 0 \Leftrightarrow f'\left( x \right) - 2 = 0 \Leftrightarrow f'\left( x \right) = 2 \Leftrightarrow \left[ \begin{array}{l}x = {x_1}\\x = 0\\x = {x_2}\end{array} \right.\)
Bảng biến thiên:
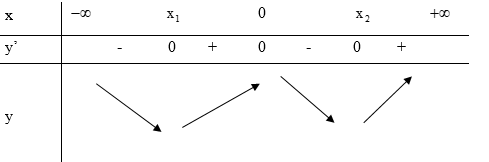
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận