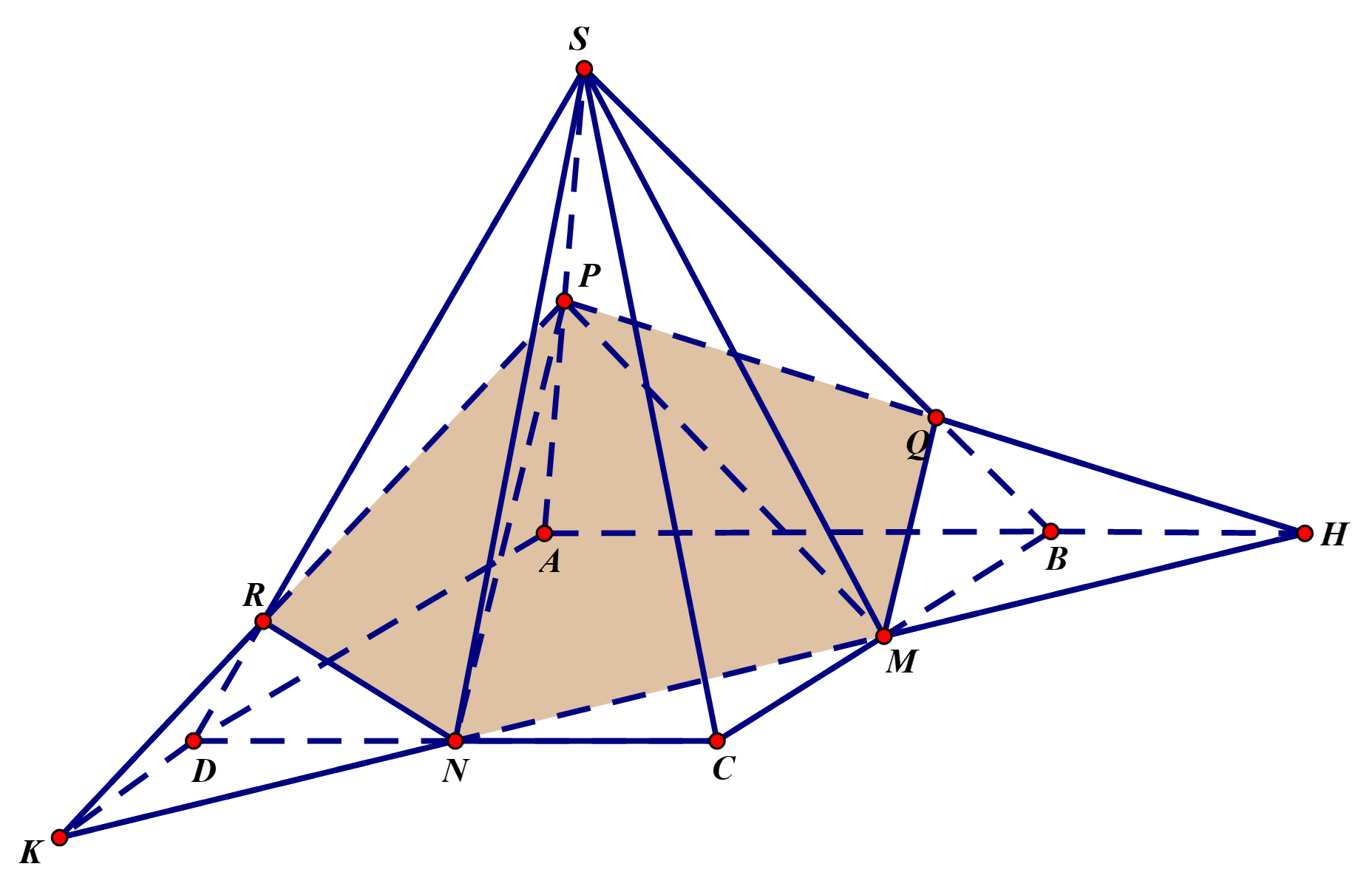
Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Gọi \(M\), \(N\) và \(P\) lần lượt là trung điểm của các đoạn \(BC\), \(CD\) và \(SA\). Mặt phẳng \(\left( {MNP} \right)\) chia khối chóp thành hai phần có thể tích lần lượt là \({V_1}\) và \({V_2}\). Biết rằng \({V_1} \le {V_2}\), tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}.\)
A. \(1\).
B. \(\frac{1}{2}\).
C. \(\frac{5}{6}\).
D. \(\frac{2}{3}\).
Câu hỏi trong đề: Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải
Chọn A
Ta có \(BH = \frac{1}{3}AH\) suy ra \(B\) là trọng tâm của tam giác \(SAT\).
Do đó, \(\frac{{BQ}}{{BU}} = \frac{{BH}}{{AB}} = \frac{1}{2} \Rightarrow \frac{{BQ}}{{BS}} = \frac{1}{4}\). Tương tự ta có, \(\frac{{DR}}{{SD}} = \frac{1}{4}\).
\(\frac{{{V_{S.PRN}}}}{{{V_{S.ADN}}}} = \frac{{SP}}{{SA}}.\frac{{SR}}{{SD}} = \frac{1}{2}.\frac{3}{4} = \frac{3}{8} \Rightarrow \frac{{{V_{S.PRN}}}}{{{V_{S.ABCD}}}} = \frac{3}{{32}}\).
Tương tự, ta có \(\frac{{{V_{S.PQM}}}}{{{V_{S.ABCD}}}} = \frac{3}{{32}}\).
Lại có \(\frac{{{V_{S.PMN}}}}{{{V_{S.AMN}}}} = \frac{{SP}}{{SA}} = \frac{1}{2} \Rightarrow \frac{{{V_{S.PMN}}}}{{{V_{S.ABCD}}}} = \frac{3}{{16}}\).
\(\frac{{{V_{S.MNC}}}}{{{V_{S.ABCD}}}} = \frac{1}{8}\).
Suy ra thể tích khối đa diện chứa đỉnh \(S\) là \({V_1} = \left( {\frac{3}{{32}} + \frac{3}{{32}} + \frac{3}{{16}} + \frac{1}{8}} \right){V_{SABCD}} = \frac{1}{2}{V_{SABCD}}\).
Vậy \(\frac{{{V_1}}}{{{V_2}}} = 1\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(y = - {x^4} + 3{x^2} + 1\).
B. \(y = - {x^4} + 2{x^2}\).
C. \(y = {x^4} + 3{x^2} - 2\).
D. \(y = - {x^4} + 2{x^2} + 1\).
Lời giải
Lời giải
Chọn D
Từ đồ thị ta có hàm bậc \(4\) trùng phương \(y = a{x^4} + b{x^2} + c.\)
Từ đồ thị ta có \(a < 0\) nên loại C
Từ đồ thị ta có \(x = 0 \Rightarrow y = 1\) nên loại B
Từ đồ thị ta có \(x = 1 \Rightarrow y = 2\) nên loại D
Câu 2
A. \(m = - 2\).
B. \(m = 4\).
C. \(m = - \frac{1}{2}\).
D. \(m = 1\).
Lời giải
Lời giải
Chọn B
Xét hàm số \(y = \frac{{mx - 3}}{{x - 4m}}\).
Tập xác định \(D = \mathbb{R}\backslash \left\{ {4m} \right\}\).
Ta có \(\mathop {{\rm{lim}}}\limits_{x \to - \infty } y = \mathop {{\rm{lim}}}\limits_{x \to + \infty } y = m\).
Do đó đồ thị hàm số có tiệm cận ngang là đường thẳng \(d:y = m\).
\(A\left( { - 2;4} \right) \in d\) nên \(m = 4\).
Câu 3
A. \[y = {x^3} - 3{x^2} - 2\].
B. \[y = - {x^3} + 3{x^2} - 1\].
C. \[y = {x^3} - 3{x^2} + 2\].
D. \[y = {x^3} + 3{x^2} - 1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\left( {0; + \infty } \right)\)
B. \(\left( { - \infty ;0} \right]\)
C. \(\emptyset \)
D. \(\left[ {0; + \infty } \right)\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2\).
B. \(4\).
C. \(3\).
D. \(0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(y = - 2\).
B. \(y = 2\).
C. \(x = 1\).
D. \(x = - 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập