Nhân ngày 20 tháng 10 một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiện của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy Thu Ngân:
a) Chị Hoa không có thẻ khách hàng thân thiện của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1 050 000 đồng. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?
b) Cô Hà có thẻ khách hàng thân thiện, cô mua 1 chiếc túi xách và nhận được một voucher trị giá 91 000 đồng. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?
Nhân ngày 20 tháng 10 một cửa hàng thời trang giảm 30% giá niêm yết cho tất cả sản phẩm. Đặc biệt nếu khách hàng nào có thẻ khách hàng thân thiện của cửa hàng thì được tặng thêm một voucher trị giá bằng 10% số tiền thanh toán tại quầy Thu Ngân:
a) Chị Hoa không có thẻ khách hàng thân thiện của cửa hàng, chị mua một chiếc váy có giá niêm yết là 1 050 000 đồng. Hỏi chị Hoa phải trả bao nhiêu tiền cho chiếc váy đó?
b) Cô Hà có thẻ khách hàng thân thiện, cô mua 1 chiếc túi xách và nhận được một voucher trị giá 91 000 đồng. Hỏi giá niêm yết ban đầu của túi xách là bao nhiêu?
Quảng cáo
Trả lời:
Lời giải
a) Chị Hoa phải trả số tiền là:
1 050 000 – 1 050 000 × 30% = 735 000 (đồng)
b) Giá chiếc túi đã giảm khi có thẻ khách hàng thân thiết là:
91 000 : 10% = 910 000 (đồng)
Giá chiếc túi ban đầu là:
910 000 : (1 – 30%) = 1 300 000 (đồng)
Vậy giá niêm yết ban đầu của túi xách là 1 300 000 đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Ta có:
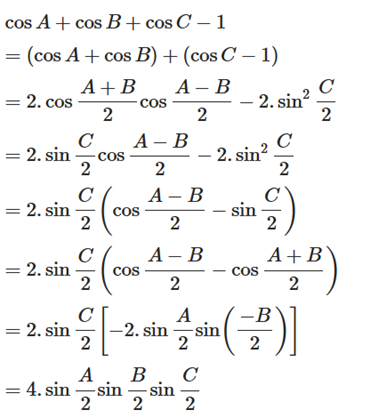
Suy ra \[{\rm{cosA + cosB + cosC = 1 + 4}}\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\]
Vậy \[{\rm{cosA + cosB + cosC = 1 + 4}}\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\].
Lời giải
Lời giải

a) Vì tam giác ACO vuông tại A
Nên \(\widehat {AOC} + \widehat {AC{\rm{O}}} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Ta có: \(\widehat {AOC} + \widehat {CD{\rm{O}}} + \widehat {DOB} = 180^\circ \)
Hay \(\widehat {AOC} + \widehat {DOB} = 180^\circ - \widehat {CD{\rm{O}}} = 180^\circ - 90^\circ = 90^\circ \)
Suy ra \(\widehat {BO{\rm{D}}} = \widehat {AC{\rm{O}}}\)
Xét ∆ACO và ∆BDO có
\(\widehat {CAO} = \widehat {DBO}\left( { = 90^\circ } \right)\)
\(\widehat {BO{\rm{D}}} = \widehat {AC{\rm{O}}}\) (Chứng minh trên)
Suy ra (g.g)
b) Gọi E là giao điểm của CO và BD
Xét ∆ACO và ∆BEO có
\(\widehat {CAO} = \widehat {EBO}\left( { = 90^\circ } \right)\)
AO = BO (giả thiết)
\(\widehat {BOE} = \widehat {AOC}\) (hai góc đối đỉnh)
Suy ra ∆ACO và ∆BEO (g.c.g)
Do đó AC = BE, CO = OE (các cặp cạnh tương ứng)
Xét ∆COD và ∆EOD có
OD là cạnh chung;
\(\widehat {CO{\rm{D}}} = \widehat {EOD}\left( { = 90^\circ } \right)\);
CO = OE (chứng minh trên)
Suy ra ∆COD và ∆EOD (c.g.c)
Do đó CD = DE (hai cạnh tương ứng)
Ta có CD = DE = BD + BE = BD + AC
Vậy CD = AC + BD
c) Ta có AC ⊥ AB và DB ⊥ AB
Suy ra AC // BD
Do đó \(\widehat {CAN} = \widehat {N{\rm{D}}B}\) (hai góc so le trong)
Xét ∆ANC và ∆DNB có
\(\widehat {ANC} = \widehat {BN{\rm{D}}}\) (hai góc đối đỉnh)
\(\widehat {CAN} = \widehat {N{\rm{D}}B}\) (Chứng minh trên)
Suy ra (g.g)
Do đó \(\frac{{AN}}{{ND}} = \frac{{AC}}{{B{\rm{D}}}}\)
Mà AC = BE nên \(\frac{{AN}}{{ND}} = \frac{{BE}}{{B{\rm{D}}}}\)
Ta có DC = DE (chứng minh câu a)
Suy ra tam giác DCE cân ở D
Mà DO là đường cao
Nên DO là phân giác của \(\widehat {C{\rm{D}}E}\)
Suy ra \(\widehat {{\rm{CD}}O} = \widehat {O{\rm{D}}E}\)
Xét ∆MOD và ∆BOD có
\(\widehat {{\rm{DMO}}} = \widehat {DBO}\left( { = 90^\circ } \right)\)
OD là cạnh chung
\(\widehat {{\rm{MD}}O} = \widehat {O{\rm{DB}}}\) (chứng minh trên)
Suy ra ∆MOD = ∆BOD (cạnh huyền – góc nhọn)
Do đó MD = BD, OM = OB
Mà OB = OA nên OM = OA
Xét ∆MOC và ∆AOC có
\(\widehat {{\rm{CMO}}} = \widehat {CAO}\left( { = 90^\circ } \right)\)
OC là cạnh chung
OM = OA (chứng minh trên)
Suy ra ∆MOC = ∆AOC (cạnh huyền – cạnh góc vuông)
Do đó MC = AC
Khi đó: \(\frac{{AN}}{{ND}} = \frac{{BE}}{{B{\rm{D}}}} = \frac{{AC}}{{BD}} = \frac{{CM}}{{DM}}\)
Suy ra MN // AC (định lí Talet đảo)
Vậy MN // AC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.