Cho A = (2m – 1; m + 3) và B = (–4; 5). Tìm m sao cho
a) A là tập hợp con của B.
b) B là tập hợp con của A.
c) A ∩ B = ∅.
Cho A = (2m – 1; m + 3) và B = (–4; 5). Tìm m sao cho
a) A là tập hợp con của B.
b) B là tập hợp con của A.
c) A ∩ B = ∅.
Quảng cáo
Trả lời:
Lời giải
a) Ta có:
\[{\rm{A}} \subset B \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \ge - 4\\m + 3 \le 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m \ge - 3\\m \le 2\end{array} \right. \Leftrightarrow \frac{{ - 3}}{2} \le m \le 2\].
b) Ta có:
\[B \subset A \Leftrightarrow \left\{ \begin{array}{l}2m - 1 \le - 4\\m + 3 \ge 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m \le - 3\\m \ge 2\end{array} \right. \Leftrightarrow m \in \emptyset \].
c) Ta có:
\(A \cap B = \emptyset \Leftrightarrow \left[ \begin{array}{l}m + 3 < 4\\2m - 1 > 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 1\\m > 3\end{array} \right.\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
Ta có:
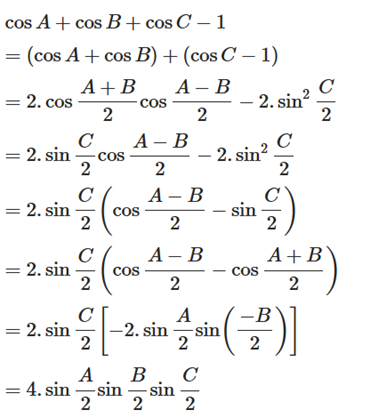
Suy ra \[{\rm{cosA + cosB + cosC = 1 + 4}}\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\]
Vậy \[{\rm{cosA + cosB + cosC = 1 + 4}}\sin \frac{A}{2}\sin \frac{B}{2}\sin \frac{C}{2}\].
Lời giải
Lời giải

a) Vì tam giác ACO vuông tại A
Nên \(\widehat {AOC} + \widehat {AC{\rm{O}}} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Ta có: \(\widehat {AOC} + \widehat {CD{\rm{O}}} + \widehat {DOB} = 180^\circ \)
Hay \(\widehat {AOC} + \widehat {DOB} = 180^\circ - \widehat {CD{\rm{O}}} = 180^\circ - 90^\circ = 90^\circ \)
Suy ra \(\widehat {BO{\rm{D}}} = \widehat {AC{\rm{O}}}\)
Xét ∆ACO và ∆BDO có
\(\widehat {CAO} = \widehat {DBO}\left( { = 90^\circ } \right)\)
\(\widehat {BO{\rm{D}}} = \widehat {AC{\rm{O}}}\) (Chứng minh trên)
Suy ra (g.g)
b) Gọi E là giao điểm của CO và BD
Xét ∆ACO và ∆BEO có
\(\widehat {CAO} = \widehat {EBO}\left( { = 90^\circ } \right)\)
AO = BO (giả thiết)
\(\widehat {BOE} = \widehat {AOC}\) (hai góc đối đỉnh)
Suy ra ∆ACO và ∆BEO (g.c.g)
Do đó AC = BE, CO = OE (các cặp cạnh tương ứng)
Xét ∆COD và ∆EOD có
OD là cạnh chung;
\(\widehat {CO{\rm{D}}} = \widehat {EOD}\left( { = 90^\circ } \right)\);
CO = OE (chứng minh trên)
Suy ra ∆COD và ∆EOD (c.g.c)
Do đó CD = DE (hai cạnh tương ứng)
Ta có CD = DE = BD + BE = BD + AC
Vậy CD = AC + BD
c) Ta có AC ⊥ AB và DB ⊥ AB
Suy ra AC // BD
Do đó \(\widehat {CAN} = \widehat {N{\rm{D}}B}\) (hai góc so le trong)
Xét ∆ANC và ∆DNB có
\(\widehat {ANC} = \widehat {BN{\rm{D}}}\) (hai góc đối đỉnh)
\(\widehat {CAN} = \widehat {N{\rm{D}}B}\) (Chứng minh trên)
Suy ra (g.g)
Do đó \(\frac{{AN}}{{ND}} = \frac{{AC}}{{B{\rm{D}}}}\)
Mà AC = BE nên \(\frac{{AN}}{{ND}} = \frac{{BE}}{{B{\rm{D}}}}\)
Ta có DC = DE (chứng minh câu a)
Suy ra tam giác DCE cân ở D
Mà DO là đường cao
Nên DO là phân giác của \(\widehat {C{\rm{D}}E}\)
Suy ra \(\widehat {{\rm{CD}}O} = \widehat {O{\rm{D}}E}\)
Xét ∆MOD và ∆BOD có
\(\widehat {{\rm{DMO}}} = \widehat {DBO}\left( { = 90^\circ } \right)\)
OD là cạnh chung
\(\widehat {{\rm{MD}}O} = \widehat {O{\rm{DB}}}\) (chứng minh trên)
Suy ra ∆MOD = ∆BOD (cạnh huyền – góc nhọn)
Do đó MD = BD, OM = OB
Mà OB = OA nên OM = OA
Xét ∆MOC và ∆AOC có
\(\widehat {{\rm{CMO}}} = \widehat {CAO}\left( { = 90^\circ } \right)\)
OC là cạnh chung
OM = OA (chứng minh trên)
Suy ra ∆MOC = ∆AOC (cạnh huyền – cạnh góc vuông)
Do đó MC = AC
Khi đó: \(\frac{{AN}}{{ND}} = \frac{{BE}}{{B{\rm{D}}}} = \frac{{AC}}{{BD}} = \frac{{CM}}{{DM}}\)
Suy ra MN // AC (định lí Talet đảo)
Vậy MN // AC.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.