Câu hỏi:
13/07/2024 1,251
Cho hàm số y = cot x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).
x
\(\frac{\pi }{6}\)
\(\frac{\pi }{4}\)
\(\frac{\pi }{3}\)
\(\frac{\pi }{2}\)
\(\frac{{2\pi }}{3}\)
\(\frac{{3\pi }}{4}\)
\(\frac{{5\pi }}{6}\)
y = cot x
?
?
?
?
?
?
?
Bằng cách lấy nhiều điểm M(x; cot x) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cot x trên khoảng (0; π).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = cot x như hình dưới đây.
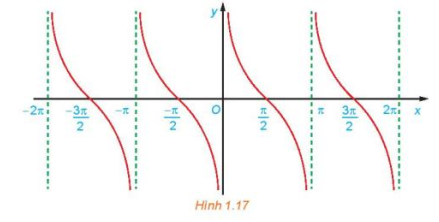
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số y = cotx.
Cho hàm số y = cot x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).
|
x |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
\(\frac{\pi }{2}\) |
\(\frac{{2\pi }}{3}\) |
\(\frac{{3\pi }}{4}\) |
\(\frac{{5\pi }}{6}\) |
|
y = cot x |
? |
? |
? |
? |
? |
? |
? |
Bằng cách lấy nhiều điểm M(x; cot x) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cot x trên khoảng (0; π).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = cot x như hình dưới đây.
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số y = cotx.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải: a) Hàm số y = f(x) = cot x có tập xác định là D = ℝ \ {kπ | k ∈ ℤ}.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cot (– x) = – cot x = – f(x), ∀ x ∈ D.
Vậy y = cot x là hàm số lẻ.
b) Ta có: \(\cot \frac{\pi }{6} = \sqrt 3 ,\cot \frac{\pi }{4} = 1,\,\cot \frac{\pi }{3} = \frac{{\sqrt 3 }}{3},\cot \frac{\pi }{2} = 0\),
\(\cot \frac{{2\pi }}{3} = - \frac{{\sqrt 3 }}{3},\cot \frac{{3\pi }}{4} = - 1,\,\cot \frac{{5\pi }}{6} = - \sqrt 3 \).
Vậy ta hoàn thành được bảng như sau:
|
x |
\(\frac{\pi }{6}\) |
\(\frac{\pi }{4}\) |
\(\frac{\pi }{3}\) |
\(\frac{\pi }{2}\) |
\(\frac{{2\pi }}{3}\) |
\(\frac{{3\pi }}{4}\) |
\(\frac{{5\pi }}{6}\) |
|
y = cot x |
\(\sqrt 3 \) |
1 |
\(\frac{{\sqrt 3 }}{3}\) |
0 |
\( - \frac{{\sqrt 3 }}{3}\) |
– 1 |
\( - \sqrt 3 \) |
c) Quan sát Hình 1.17, ta thấy đồ thị hàm số y = cot x có:
+) Tập giá trị là ℝ;
+) Nghịch biến trên mỗi khoảng \(\left( {k\pi ;\,\pi + k\pi } \right),\,k \in \mathbb{Z}\) (do đồ thị hàm số đi xuống từ trái sang phải trên mỗi khoảng này).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
a) Chu kì của sóng là \(T = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20\) (giây).
b) Ta có: h(t) = \(90\cos \left( {\frac{\pi }{{10}}.t} \right)\), hàm số này có giá trị lớn nhất và nhỏ nhất lần lượt là 90 và – 90.
Vậy chiều cao của sóng là 180 cm.
Lời giải
Lời giải:
a) Biểu thức sin 2x + tan 2x có nghĩa khi cos 2x ≠ 0 (do \(\tan 2x = \frac{{\sin 2x}}{{\cos 2x}}\)), tức là \(2x \ne \frac{\pi }{2} + k\pi ,k \in \mathbb{Z}\) \( \Leftrightarrow x \ne \frac{\pi }{4} + k\frac{\pi }{2},k \in \mathbb{Z}\).
Suy ra tập xác định của hàm số y = f(x) = sin 2x + tan 2x là \(D = \mathbb{R}\backslash \left\{ {\frac{\pi }{4} + k\frac{\pi }{2}|k \in \mathbb{Z}} \right\}\).
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– 2x) + tan (– 2x) = – sin 2x – tan 2x = – (sin 2x + tan 2x) = – f(x), ∀ x ∈ D.
Vậy y = sin 2x + tan 2x là hàm số lẻ.
b) Tập xác định của hàm số y = f(x) = cos x + sin2 x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = cos (– x) + sin2 (– x) = cos x + (– sin x)2 = cos x + sin2 x = f(x), ∀ x ∈ D.
Vậy y = cos x + sin2 x là hàm số chẵn.
c) Tập xác định của hàm số y = f(x) = sin x cos 2x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) . cos (– 2x) = – sin x . cos 2x = – f(x), ∀ x ∈ D.
Vậy y = sin x cos 2x là hàm số lẻ.
d) Tập xác định của hàm số y = f(x) = sin x + cos x là D = ℝ.
Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.
Ta có: f(– x) = sin (– x) + cos (– x) = – sin x + cos x ≠ – f(x).
Vậy y = sin x + cos x là hàm số không chẵn, không lẻ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
10 Bài tập Nhận biết góc phẳng của góc nhị diện và tính góc phẳng nhị diện (có lời giải)
-
Bài tập Hình học không gian lớp 11 cơ bản, nâng cao có lời giải (P11)
-
Bài tập Xác suất ôn thi THPT Quốc gia có lời giải (P1)
-
38 câu trắc nghiệm Toán 11 Kết nối tri thức Lôgarit có đáp án
-
12 câu Trắc nghiệm Toán 11 Kết nối tri thức Giá trị lượng giác của góc lượng giác có đáp án
-
15 câu Trắc nghiệm Khoảng cách có đáp án (Nhận biết)
-
Bài tập Tổ hợp - Xác suất cơ bản, nâng cao có lời giải chi tiết (P6)
-
10 Bài tập Biến cố hợp. Biến cố giao (có lời giải)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận