Câu hỏi:
13/07/2024 1,783
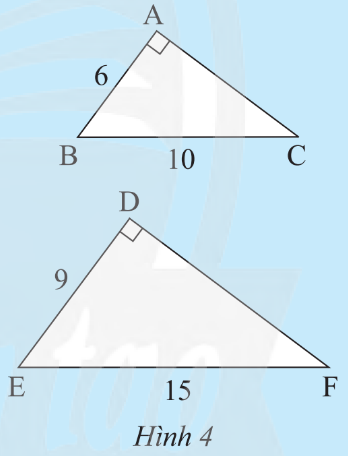
Cho hai tam giác vuông ABC và DEF có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh AC và DF.
b) So sánh các tỉ số \[\frac{{AB}}{{DE}},\frac{{AC}}{{DF}}\;\] và \[\frac{{BC}}{{EF}}\].
c) Dự đoán sự đồng dạng của hai tam giác ABC và DEF.
Cho hai tam giác vuông ABC và DEF có các kích thước như Hình 4.
a) Hãy tính độ dài cạnh AC và DF.
b) So sánh các tỉ số \[\frac{{AB}}{{DE}},\frac{{AC}}{{DF}}\;\] và \[\frac{{BC}}{{EF}}\].
c) Dự đoán sự đồng dạng của hai tam giác ABC và DEF.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lời giải:
a) Áp dụng định lí Pythagore cho tam giác vuông ABC, ta có:
BC2 = AB2 + AC2
Suy ra AC2 = BC2 – AB2 = 102 – 62 = 64
Do đó AC = 8.
Áp dụng định lí Pythagore cho tam giác vuông DEF, ta có:
EF2 = DE2 + DF2
Suy ra DF2 = EF2 – DE2 = 152 – 92 = 144.
Do đó DF = 12.
b) Ta có: \[\frac{{AB}}{{DE}} = \frac{6}{9} = \frac{2}{3},\;\frac{{AC}}{{DF}} = \frac{8}{{12}} = \frac{2}{3},\;\frac{{BC}}{{EF}} = \frac{{10}}{{15}} = \frac{2}{3}\].
Suy ra \[\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\].
c) Xét ΔABC và ΔDEF có: \[\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}}\] (câu b).
Dự đoán: ΔABC ᔕ ΔDEF.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải:
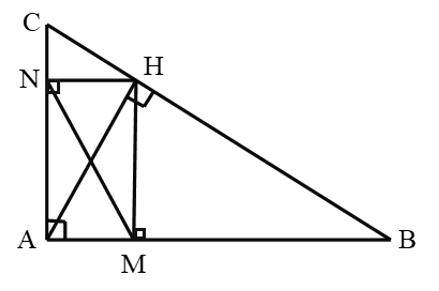
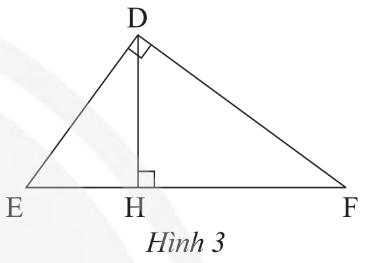
a) Xét hai tam giác vuông AMH và AHB có: \[\widehat A\] chung
Suy ra ΔAMH ᔕ ΔAHB (g.g)
b) ΔAMH ᔕ ΔAHB nên \[\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\;\] hay AM.AB = AH2 (1)
Xét hai tam giác vuông ANH và AHC có: \[\widehat A\] chung
Suy ra ΔANH ᔕ ΔAHC (g.g) nên \[\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\;\] hay AN.AC = AH2 (2)
Từ (1) và (2) suy ra AM.AB = AN.AC (đpcm).
c) Ta có AM.AB = AN.AC, do đó \[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\].
Xét hai tam giác vuông AMN và ABC có:
\[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}}\] (chứng minh trên)
Do đó ΔANM ᔕ ΔABC (c.g.c)
d) Áp dụng định lí Pythagore vào tam giác ABC, ta có:
BC2 = AB2 + AC2 = 92 + 122 = 225.
Suy ra BC = 15 cm.
Xét hai tam giác vuông ABC và HBA có \(\widehat B\) chung
Do đó ΔABC ᔕ ΔHBA (g.g).
Suy ra \[\frac{{AC}}{{AH}} = \frac{{BC}}{{AB}}\] (các cặp cạnh tương ứng).
Khi đó AH.BC = AB.AC hay AH.15 = 9.12.
Suy ra AH = 7,2 cm.
• Từ (1): AM.AB = AH2 nên \[AM = \frac{{A{H^2}}}{{AB}} = \frac{{7,{2^2}}}{9} = 5,76\,\,(cm)\]
• Từ (2): AN.AC = AH2 nên \[AN = \frac{{A{H^2}}}{{AC}} = \frac{{7,{2^2}}}{{12}} = 4,32\,\,(cm)\]
Diện tích tam giác AMN là:
\[\frac{1}{2}\,.\,5,76\,.\,4,32 = 12,4416\,\,(c{m^2})\].
Vậy diện tích tam giác AMN là 12,4416 cm2.
Lời giải
Lời giải:
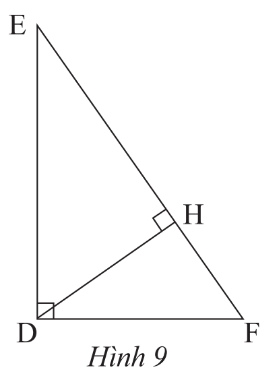
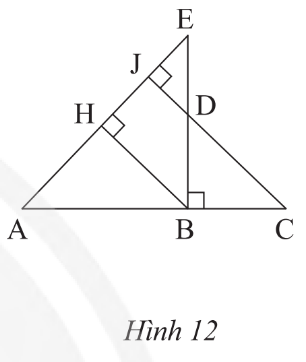
Tam giác HED vuông tại H và tam giác DEF vuông tại D có chung
Do đó ΔHED ᔕ ΔDEF (g.g)
Suy ra (các cạnh tương ứng).
Do đó DE2 = EH.EF (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 25
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Đề cuối kì 2 Toán 8 Cánh diều cấu trúc mới có đáp án- Đề 2