Câu hỏi:
13/07/2024 339
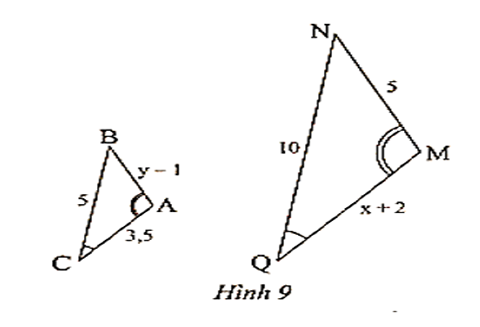
Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6. Chứng minh rằng: ∆ANM ᔕ ∆ABC.
Cho tam giác ABC có AB = 12, AC = 15. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh AC sao cho AM = 7,5 , AN = 6. Chứng minh rằng: ∆ANM ᔕ ∆ABC.
Quảng cáo
Trả lời:
Giải bởi Vietjack
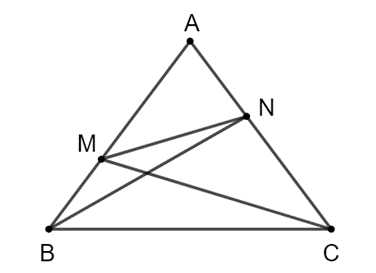
Xét ∆ANM và ∆ABC có
\[\frac{{AN}}{{AB}} = \frac{{AM}}{{AC}} = \frac{1}{2}\], \[\widehat {\rm{A}}\] chung.
Do đó ∆ABC ᔕ ∆DEF (c.g.c).
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
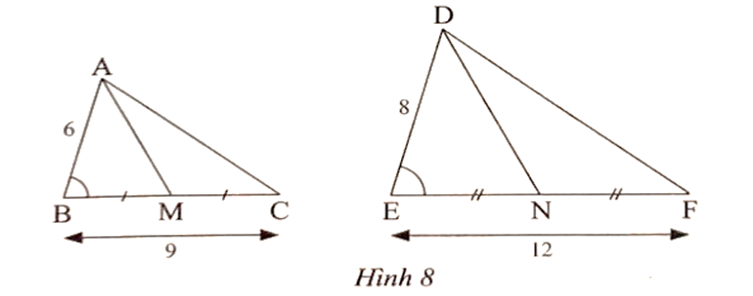
Ta có \[\frac{{AB}}{{DE}} = \frac{6}{8} = \frac{3}{4}\]; \[\frac{{BC}}{{EF}} = \frac{9}{{12}} = \frac{3}{4}\], suy ra \[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\].
Xét ∆ABC và ∆DEF có
\[\frac{{AB}}{{DE}} = \frac{{BC}}{{EF}}\]và \[\widehat B = \widehat E\]
Do đó ∆ABC ᔕ ∆DEF (c.g.c).
Lời giải
Ta có ∆AED ᔕ ∆ABC suy ra \[\frac{{AE}}{{AB}} = \frac{{AD}}{{AC}}\] hay \[\frac{{AE}}{{AD}} = \frac{{AB}}{{AC}}\] (1)
• Vì AM là tia phân giác của \[\widehat {DAE}\] nên \[\frac{{ME}}{{MD}} = \frac{{AE}}{{AD}}\] (2)
• Vì AN là tia phân giác của \[\widehat {BAC}\] nên \[\frac{{NB}}{{NC}} = \frac{{AB}}{{AC}}\] (3)
Từ (1); (2) và (3) suy ra \[\frac{{ME}}{{MD}} = \frac{{NB}}{{NC}}\] hay ME . NC = MD . NB (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
15 câu Trắc nghiệm Toán 8 Kết nối tri thức Bài 1: Đơn thức có đáp án
-
Bộ 10 đề thi cuối kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 24
-
Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 1
-
Bộ 10 đề thi giữa kì 2 Toán 8 Kết nối tri thức cấu trúc mới có đáp án (Đề 1)
-
Đề cuối kì 2 Toán 8 Chân trời sáng tạo cấu trúc mới có đáp án - Đề 1
-
15 câu Trắc nghiệm Toán 8 Cánh diều Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến có đáp án
-
15 câu Trắc nghiệm Toán 8 Chân trời sáng tạo Bài 1: Đơn thức và đa thức nhiều biến có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận