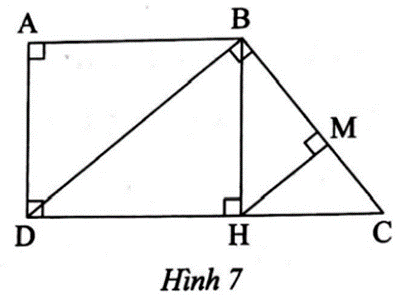
Người ta dùng một gương phẳng đề đo chiều cao của một căn nhà (Hình 9). Đặt tấm gương nằm trên mặt phẳng nằm ngang (điểm C), mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát lùi dần cho đến khi nhìn thấy ảnh của đỉnh căn nhà trong gương. Cho biết \[\widehat {ACB} = \widehat {MCN}\], AB = 1,65 m, BC = 4 m, NC = 20 m. Tính chiều cao MN của căn nhà.
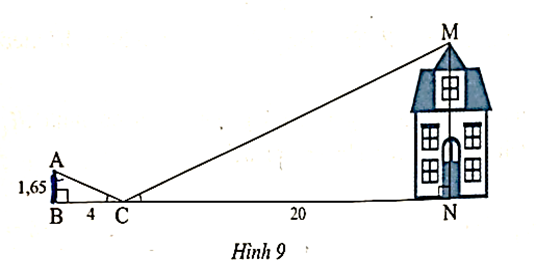
Người ta dùng một gương phẳng đề đo chiều cao của một căn nhà (Hình 9). Đặt tấm gương nằm trên mặt phẳng nằm ngang (điểm C), mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát lùi dần cho đến khi nhìn thấy ảnh của đỉnh căn nhà trong gương. Cho biết \[\widehat {ACB} = \widehat {MCN}\], AB = 1,65 m, BC = 4 m, NC = 20 m. Tính chiều cao MN của căn nhà.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét ∆ABC vuông tại B và ∆MNC vuông tại N có \[\widehat {ACB} = \widehat {MCN}\].
Do đó ∆ABC ᔕ ∆MNC (g.g).
Suy ra \[\frac{{AB}}{{MN}} = \frac{{BC}}{{NC}}\] hay \[\frac{{1,65}}{{MN}} = \frac{4}{{20}}\].
Do đó \[MN = \frac{{1,65\,.\,20}}{4} = 8,25\] (m).
Vậy chiều cao MN của căn nhà là 8,25 m.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
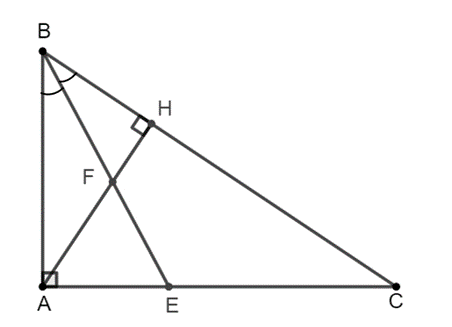
Xét ∆ABC có BE là tia phân giác của \[\widehat B\], suy ra \[\frac{{AB}}{{BC}} = \frac{{AE}}{{EC}}\] (1)
Xét ∆ABH có BF là tia phân giác của \[\widehat B\], suy ra \[\frac{{FH}}{{AF}} = \frac{{BH}}{{AB}}\] (2)
Xét ∆ABH vuông tại H và ∆ABC vuông tại A có \[\widehat B\] chung.
Do đó ∆ABH ᔕ ∆CBA, suy ra \[\frac{{AB}}{{BC}} = \frac{{BH}}{{AB}}\] (3)
Từ (1); (2) và (3) suy ra \[\frac{{AE}}{{EC}} = \frac{{FH}}{{AF}}\].
Do đó AE . AF = EC . FH.
Mà AE = AF, suy ra AE2 = EC . FH (đpcm).
Lời giải
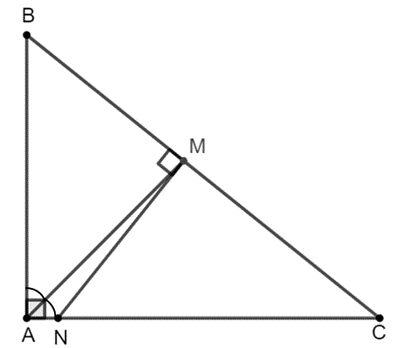
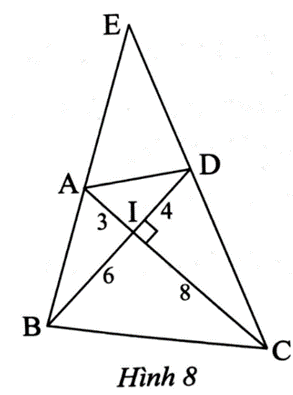
Ta có ∆MNC ᔕ ∆ABC, suy ra \[\frac{{MN}}{{AB}} = \frac{{MC}}{{AC}}\] (1)
Xét ∆ABC có AM là phân giác của \[\widehat A\] có
\[\frac{{MB}}{{MC}} = \frac{{AB}}{{AC}}\], suy ra \[\frac{{MB}}{{AB}} = \frac{{MC}}{{AC}}\] (2)
Từ (1) và (2), suy ra \[\frac{{MB}}{{AB}} = \frac{{MN}}{{AB}}\].
Do đó MN = MB (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập