Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho BD = CE. Khi đó tam giác ABC là tam giác
Cho tam giác ABC có hai đường trung tuyến BD; CE sao cho BD = CE. Khi đó tam giác ABC là tam giác
A. cân tại B;
B. cân tại C;
C. vuông tại A;
Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: D
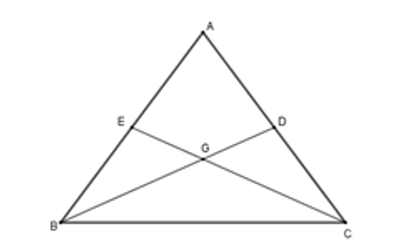
Hai đường trung tuyến BD và CE cắt nhau tại G nên G là trọng tâm của ΔABC.
Suy ra mà BD = CE
Do đó BG = CG.
Khi đó BD – BG = CE – CG hay GD = GE.
Xét ΔBGE và ΔCGD có:
BG = CG (chứng minh trên);
(hai góc đối đỉnh);
GE = GD (chứng minh trên)
Do đó ΔBGE = ΔCGD (c.g.c)
Suy ra BE = CD (hai cạnh tương ứng).
Do BD và CE là hai đường trung tuyến của ∆ABC nên D, E lần lượt là trung điểm của AC, AB. Do đó và
Mà BE = CD (chứng minh trên) nên AB = AC, suy ra tam giác ABC cân tại A.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải:
Đáp án đúng là: B
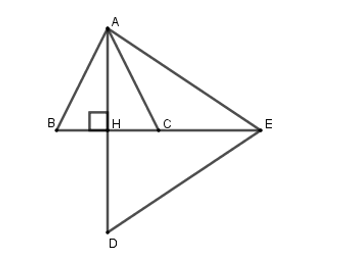
Xét ∆AHB (vuông tại H) và AHC (vuông tại H) có:
AB = AC (do ΔABC cân tại A);
AH là cạnh chung
Do đó: ΔAHB = ΔAHC (cạnh huyền – cạnh góc vuông)
Suy ra HB = HC (hai cạnh tương ứng)
Ta có CE = CB = HB + HC = 2CH
Xét ΔADE có EH là đường trung tuyến mà CE = 2CH nên C là trọng tâm của ΔADE.
Câu 2
A. GA = GB = GC;
B. GA = GB > GC;
C. GA < GB < GC;
Lời giải
Hướng dẫn giải:
Đáp án đúng là: A
Các tia AG, BG và CG cắt BC, AC, AB lần lượt tại D, E, F thì D, E, F theo thứ tự là trung điểm của BC, AC, AB.
Mà BC = AC = AB (do tam giác ABC đều).
Do đó BD = DC = CE = EA = AF = FB.
Xét ΔAEB và ΔAFC có:
AB = AC (chứng minh trên);
là góc chung
AE = AF (chứng minh trên)
Do đó ΔAEB = ΔAFC (c.g.c).
Suy ra BE = CF (hai cạnh tương ứng) (1)
Chứng minh tương tự, ta có ΔBEC = ΔADC (c.g.c).
Suy ra BE = AD (hai cạnh tương ứng) (2)
Từ (1) và (2) ta có AD = BE = CF (3)
Do G là trọng tâm của ΔABC nên ta có: (4)
Từ (3) và (4) suy ra GA = GB = GC.
Câu 3
A. 15°;
B. 30°;
C. 45°;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Ba điểm C, K, I thẳng hàng.
B. K là trọng tâm của tam giác ABC.
C. AK là đường trung tuyến của tam giác ABC;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.
B.
C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.