Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được "chu vi" của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:

1. Hồi đó, hằng năm cứ vào trưa ngày Hạ chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một cái giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.

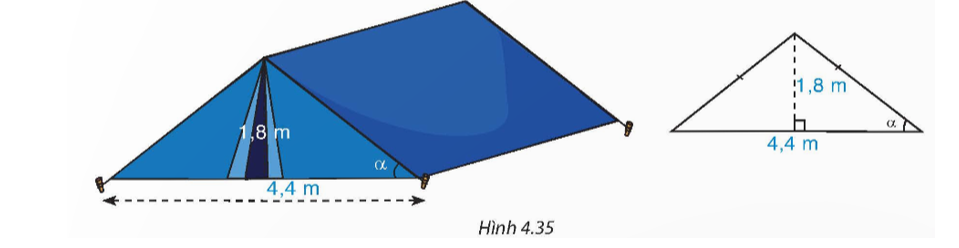
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy một tháp cao 25 m có bóng trên mặt đất dài 3,1 m.

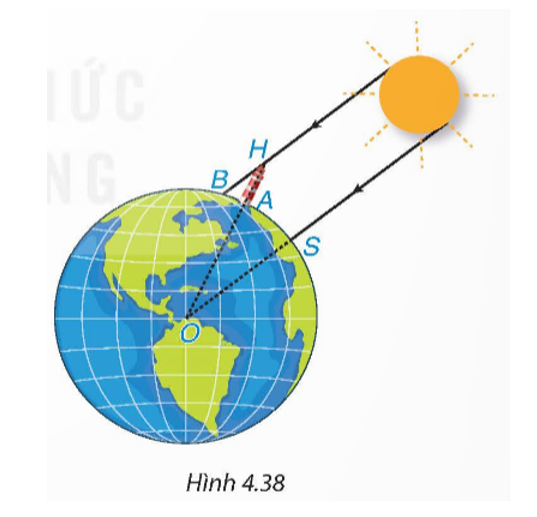
Từ hai quan sát trên, ông có thể tính xấp xỉ "chu vi" của Trái Đất như thế nào? (trên Hình 4.38, điểm O là tâm Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài tập cuối chương 4 có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Theo em, nhà toán học và thiên văn học Eratosthenes đã tính xấp xỉ "chu vi" của Trái Đất như sau:

Các tia sáng mặt trời chiếu thẳng đứng, nên ta coi các tia sáng BH, OS song song với nhau. Khi đó $\hat{A O S} = \hat{B H A}$ (hai góc so le trong).

Xét ∆ABH vuông tại A, ta có:

$\tan \hat{B H A} = \frac{A B}{A H} = \frac{3, 1}{25} = \frac{31}{250},$ suy ra $\hat{B H A} \approx 7 ° 4^{'} .$ Do đó $\hat{A O S} \approx 7 ° 4^{'} .$

Xét ∆OAS vuông tại S, ta có:

$\sin \hat{A O S} = \frac{A S}{O A},$ suy ra $O A = \frac{A S}{\sin \hat{A O S}} \approx \frac{800}{\sin 7 ° 4^{'}} \approx 6 502, 79 (km).$

Khi đó, “chu vi” của Trái Đất khoảng: 2π.OA ≈ 2 . 3,14 . 6 502,79 ≈ 40 838 (km).

Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc 20° và chắn ngang lối đi một đoạn 5 m (H.4.36). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Xem đáp án

Lời giải

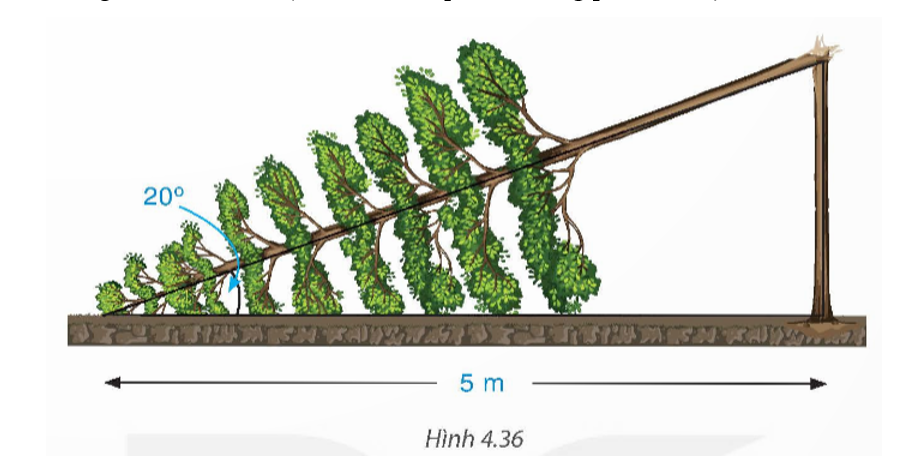
Giả sử hình ảnh cây bị gãy mô tả bởi hình vẽ như dưới đây

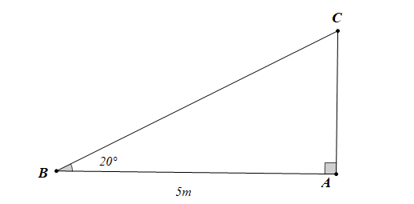
Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy (ảnh 2)

Xét ∆ABC vuông tại A, ta có:

⦁ AC = AB.tan20° = 5.tan20° ≈ 1,8 (m);

⦁ $\cos B = \frac{A B}{B C},$ suy ra $B C = \frac{A B}{cos α} = \frac{5}{cos20 °} \approx 5, 3 (m).$

Khi đó: AC + CB ≈ 1,8 + 5,3 = 7,1 (m).

Vậy trước khi bị gãy, cây cao khoảng 7,1 m.

Câu 2

Hình 4.35 là mô hình của một túp lều. Tìm góc α giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).

Xem đáp án

Lời giải

Ta có: $\tan α = \frac{1, 8}{2, 2} = \frac{9}{11},$ suy ra α ≈ 39°17’.

Vậy góc α giữa cạnh mái lều và mặt đất là khoảng 39°17’.

Câu 3