Câu hỏi:
12/07/2024 78,140
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0 (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s), cho bởi hàm số sau:
v(t) = 0,001302t3 – 0,09029t2 + 23,
(v được tính bằng ft/s, 1 feet = 0,3048 m)
(Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0 (s) cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s), cho bởi hàm số sau:
v(t) = 0,001302t3 – 0,09029t2 + 23,
(v được tính bằng ft/s, 1 feet = 0,3048 m)
(Nguồn: J. Stewart, Calculus, Seventh Edition, Brooks/Cole, CENGAGE Learning 2012)
Hỏi gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian nào tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét hàm số vận tốc của tàu con thoi v(t) = 0,001302t3 – 0,09029t2 + 23 với t ∈ [0; 126].
Gia tốc của tàu con thoi là a(t) = v'(t) = 0,003906t2 – 0,18058t.
Ta có a'(t) = 0,007812t – 0,18058
a'(t) = 0 ⇔ t ≈ 23.
Bảng biến thiên của hàm số a(t) như sau:
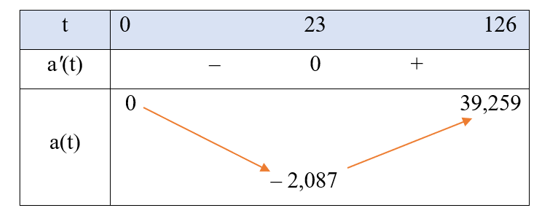
Vậy gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian (23 s; 126 s) tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi.
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có V(T) = 999,87 – 0,06426T + 0,0085043T2 – 0,0000679T3 với T ∈ [0; 30].
V'(T) = – 0,06426 + 0,0170086T – 0,0002037T2
V'(T) = 0 ⇔ T ≈ 4 hoặc T ≈ 79,5. Vì T ∈ [0; 30] nên T ≈ 4.
Ta có bảng biến thiên của hàm số như sau:
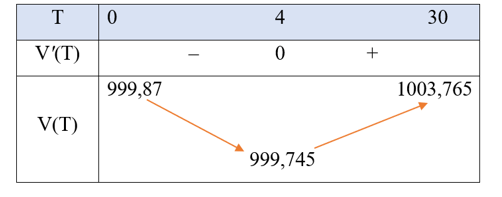
Vậy thể tích V(T) giảm trong khoảng nhiệt độ (0 ℃; 4 ℃).
Lời giải
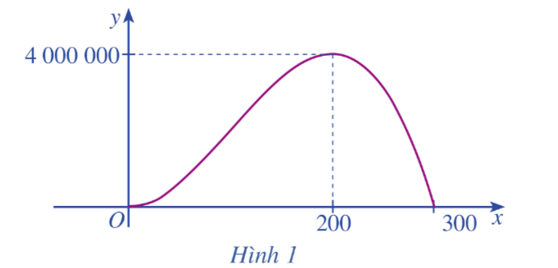
Ta có y = – x3 + 300x2 với x ∈ [0; 300].
y' = – 3x2 + 600x;
y' = 0 ⇔ x = 0 hoặc x = 200.
Bảng xét dấu của y' trên đoạn [0; 300] như sau:
Kết hợp với đồ thị ở Hình 1, ta thấy lợi nhuận theo số sản phẩm sản xuất ra tăng thì đạo hàm y' mang dấu dương, lợi nhuận theo số sản phẩm sản xuất ra giảm thì đạo hàm y' mang dấu âm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
140 câu Bài tập Hàm số mũ và Logarit cơ bản, nâng cao cực hay có lời giải chi tiết (P1)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận