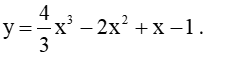Giải SGK Toán 12 Cánh diều Bài 1. Tính đơn điệu của hàm số có đáp án
29 người thi tuần này 4.6 2.2 K lượt thi 22 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp
Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm
Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận
Danh sách câu hỏi:
Lời giải
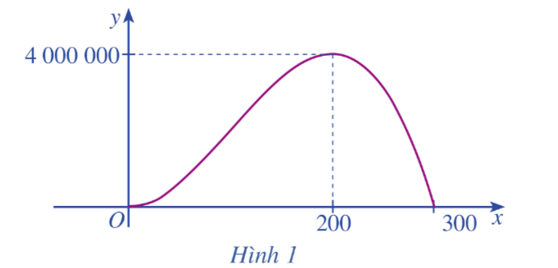
Ta có y = – x3 + 300x2 với x ∈ [0; 300].
y' = – 3x2 + 600x;
y' = 0 ⇔ x = 0 hoặc x = 200.
Bảng xét dấu của y' trên đoạn [0; 300] như sau:

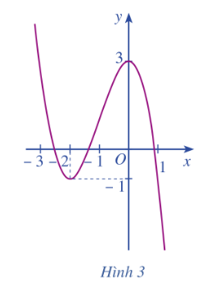
Kết hợp với đồ thị ở Hình 1, ta thấy lợi nhuận theo số sản phẩm sản xuất ra tăng thì đạo hàm y' mang dấu dương, lợi nhuận theo số sản phẩm sản xuất ra giảm thì đạo hàm y' mang dấu âm.
Lời giải
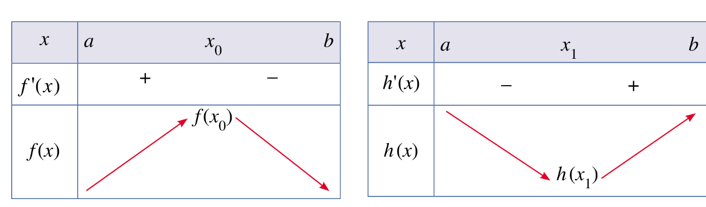
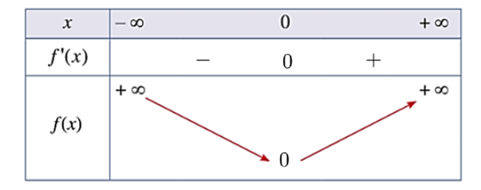
a) Cho K là một khoảng, đoạn hoặc nửa khoảng. Giả sử y = f(x) là hàm số xác định trên K. Ta nói
+ Hàm số y = f(x) được gọi là hàm số đồng biến trên K nếu với mọi x1, x2 thuộc K và x1 < x2 thì f(x1) < f(x2).
+ Hàm số y = f(x) được gọi là hàm số nghịch biến trên K nếu với mọi x1, x2 thuộc K và x1 < x2 thì f(x1) > f(x2).
Lưu ý: Nếu một hàm số đồng biến trên K thì trên đó đồ thị của nó đi lên từ trái qua phải; nếu một hàm số nghịch biến trên K thì trên đó đồ thị của nó đi xuống từ trái qua phải.
b)
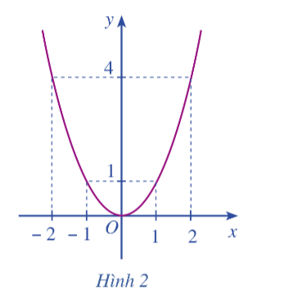
Quan sát Hình 2 ta thấy
+ Trên khoảng (– ∞; 0), đồ thị hàm số y = f(x) = x2 đi xuống từ trái qua phải nên hàm số này nghịch biến trên khoảng (– ∞; 0).
+ Trên khoảng (0; + ∞), đồ thị hàm số y = f(x) = x2 đi lên từ trái qua phải nên hàm số này đồng biến trên khoảng (0; + ∞).
Ta có 2x > 0 với mọi x ∈ (0; + ∞) và 2x < 0 với mọi x ∈ (– ∞; 0).
Do đó, f'(x) > 0 với mọi x ∈ (0; + ∞) và f'(x) < 0 với mọi x ∈ (– ∞; 0).
Mối liên hệ:
+ Trên khoảng (– ∞; 0), hàm số f(x) nghịch biến và f'(x) < 0.
+ Trên khoảng (0; + ∞), hàm số f(x) đồng biến và f'(x) > 0.
Với x = 0, ta có f(0) = 02 = 0 và f'(0) = 2 ∙ 0 = 0.
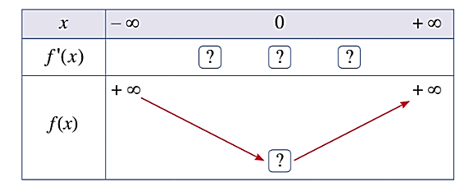
Bảng biến thiên:
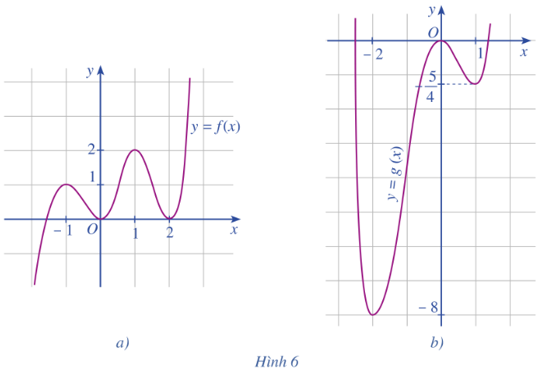
Lời giải
Hướng dẫn giải
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = 4x2 – 4x + 1;
y' = 0 ⇔ 4x2 – 4x + 1 = 0 ⇔ (2x – 1)2 = 0 ⇔ x = .
Ta có bảng xét dấu của y' như sau:
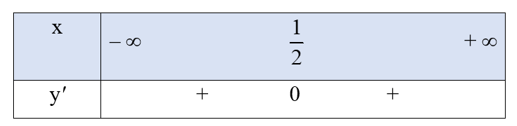
Vậy hàm số đồng biến trên mỗi khoảng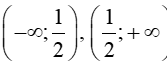
Lời giải
Hàm số đã cho có tập xác định là ℝ.
Ta có y' = 4x3 + 4x;
y' = 0 ⇔ 4x3 + 4x = 0 ⇔ x(x2 + 1) = 0 ⇔ x = 0 (do x2 + 1 > 0 với mọi x).
Bảng biến thiên của hàm số như sau:
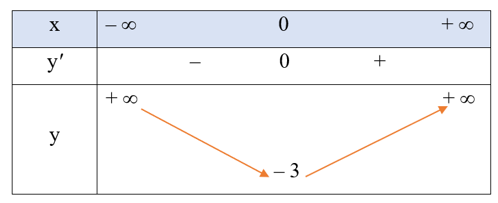
Vậy hàm số đồng biến trên khoảng (0; + ∞) và nghịch biến trên khoảng (– ∞; 0).
Lời giải
a)
Hàm số đã cho có tập xác định là ℝ.
Ta có f'(x) = 3x2;
f'(x) = 0 ⇔ 3x2 = 0 ⇔ x = 0.
Ta có bảng xét dấu của f'(x) như sau:

Vậy hàm số đồng biến trên các khoảng (– ∞; 0) và (0; + ∞).
b) Ta có f'(x) = 3x2 ≥ 0 với mọi x ∈ ℝ.
c) Phương trình f'(x) = 0 có 1 nghiệm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.