Cho hai hàm số y = f(x), y = g(x) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
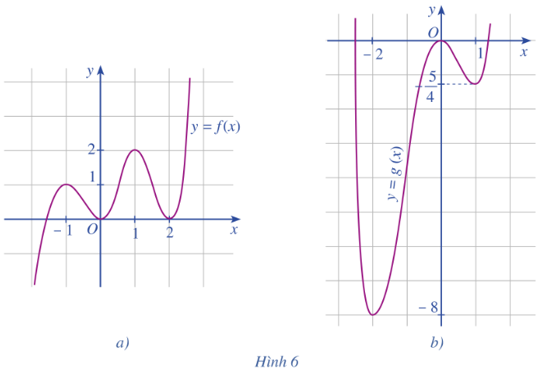
Cho hai hàm số y = f(x), y = g(x) có đồ thị lần lượt được cho ở Hình 6a, Hình 6b. Nêu khoảng đồng biến, nghịch biến và điểm cực trị của mỗi hàm số đó.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hình 6a:
– Khoảng đồng biến, nghịch biến:
Quan sát hình vẽ ta thấy:
+ Trên các khoảng (– ∞; – 1), (0; 1), (2; + ∞), đồ thị hàm số y = f(x) đi lên từ trái qua phải, do đó hàm số y = f(x) đồng biến trên mỗi khoảng (– ∞; – 1), (0; 1), (2; + ∞).
+ Trên các khoảng (– 1; 0), (1; 2), đồ thị hàm số y = f(x) đi xuống từ trái qua phải, do đó hàm số y = f(x) nghịch biến trên mỗi khoảng (– 1; 0) và (1; 2).
– Điểm cực trị:
+ Xét khoảng (– ∞; 0) chứa điểm x = – 1. Quan sát đồ thị hàm số y = f(x) ở Hình 6a, ta thấy f(x) < f(– 1) với mọi x ∈ (– ∞; 0) và x ≠ – 1. Do đó, x = – 1 là một điểm cực đại của hàm số y = f(x).
Tương tự, ta thấy f(x) < f(1) với mọi x ∈ (0; 2) và x ≠ 1. Do đó, x = 1 là một điểm cực đại của hàm số y = f(x).
+ Xét khoảng (– 1; 1) chứa điểm x = 0. Quan sát đồ thị hàm số ta thấy f(x) > f(0) với mọi x ∈ (– 1; 1) và x ≠ 0. Do đó, x = 0 là một điểm cực tiểu của hàm số y = f(x).
Tương tự, ta thấy f(x) > f(2) với mọi x ∈ (1; + ∞) và x ≠ 2. Vậy x = 2 là một điểm cực tiểu của hàm số y = f(x).
Hình 6b:
– Khoảng đồng biến, nghịch biến:
Quan sát hình vẽ ta thấy:
+ Trên các khoảng (– 2; 0), (1; + ∞), đồ thị hàm số y = g(x) đi lên từ trái qua phải nên hàm số này đồng biến trên mỗi khoảng (– 2; 0) và (1; + ∞).
+ Trên các khoảng (– ∞; – 2), (0; 1), đồ thị hàm số y = g(x) đi xuống từ trái qua phải nên hàm số này nghịch biến trên mỗi khoảng (– ∞; – 2) và (0; 1).
– Điểm cực trị:
+ Xét khoảng (– ∞; 0) chứa điểm x = – 2. Quan sát đồ thị hàm số y = g(x) ở Hình 6b ta thấy g(x) > g(– 2) với mọi x ∈ (– ∞; 0) và x ≠ – 2. Vậy x = – 2 là một điểm cực tiểu của hàm số y = g(x).
Tương tự, ta thấy g(x) > g(1) với mọi x ∈ (0; + ∞) và x ≠ 1. Do đó, x = 1 là một điểm cực tiểu của hàm số y = g(x).
+ Xét khoảng (– 2; 1) chứa điểm x = 0. Quan sát đồ thị hàm số y = g(x) ở Hình 6b ta thấy g(x) < g(0) với mọi x ∈ (– 2; 1) và x ≠ 0. Do đó, x = 0 là điểm cực đại của hàm số y = g(x).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Xét hàm số vận tốc của tàu con thoi v(t) = 0,001302t3 – 0,09029t2 + 23 với t ∈ [0; 126].
Gia tốc của tàu con thoi là a(t) = v'(t) = 0,003906t2 – 0,18058t.
Ta có a'(t) = 0,007812t – 0,18058
a'(t) = 0 ⇔ t ≈ 23.
Bảng biến thiên của hàm số a(t) như sau:
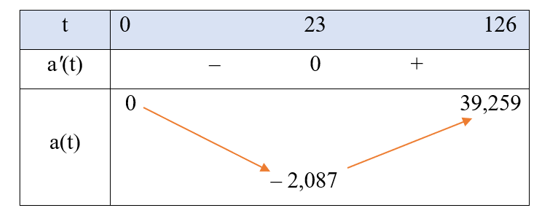
Vậy gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian (23 s; 126 s) tính từ thời điểm cất cánh cho đến khi tên lửa đẩy được phóng đi.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có V(T) = 999,87 – 0,06426T + 0,0085043T2 – 0,0000679T3 với T ∈ [0; 30].
V'(T) = – 0,06426 + 0,0170086T – 0,0002037T2
V'(T) = 0 ⇔ T ≈ 4 hoặc T ≈ 79,5. Vì T ∈ [0; 30] nên T ≈ 4.
Ta có bảng biến thiên của hàm số như sau:
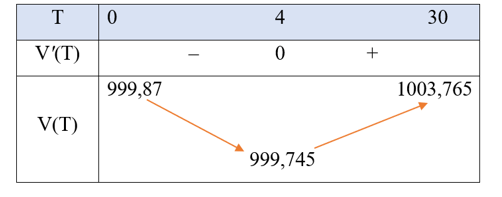
Vậy thể tích V(T) giảm trong khoảng nhiệt độ (0 ℃; 4 ℃).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập