Câu hỏi:

17/04/2024 6,788

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) y = 2x³ – 3x² + 1;

Xem lời giải

Câu hỏi trong đề: Giải SGK Toán 12 Cánh diều Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) y = 2x³ – 3x² + 1

1) Tập xác định: ℝ.

2) Sự biến thiên:

Giới hạn tại vô cực: $\lim_{x \to + \infty} y = + \infty, \lim_{x \to - \infty} y = - \infty$ .

y' = 6x² – 6x;

y' = 0 ⇔ 6x² – 6x = 0 ⇔ x = 0 hoặc x = 1.

Bảng biến thiên:

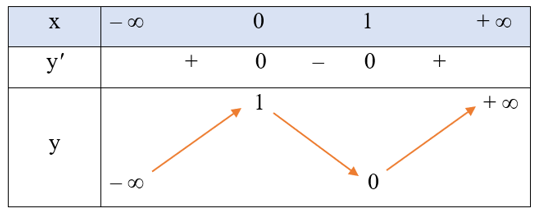
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) y = 2x^3 – 3x^2 + 1; (ảnh 1)

Hàm số đã cho đồng biến trên mỗi khoảng (– ∞; 0) và (1; + ∞); nghịch biến trên khoảng (0; 1).

Hàm số đạt cực đại tại x = 0, y_CĐ = 1; đạt cực tiểu tại x = 1, y_CT = 0.

3) Đồ thị

Giao điểm của đồ thị với trục tung: (0; 1).

Giao điểm của đồ thị với trục hoành:

Giải phương trình 2x³ – 3x² + 1 = 0 ta được x = $- \frac{1}{2}$ hoặc x = 1.

Vậy đồ thị hàm số giao với trục hoành tại các điểm $(- \frac{1}{2}; 0)$ , (1; 0).

Đồ thị hàm số đi qua các điểm (1; 0), (0; 1), $(- \frac{1}{2}; 0)$ , (– 1; – 4) và $(\frac{1}{2}; \frac{1}{2})$ .

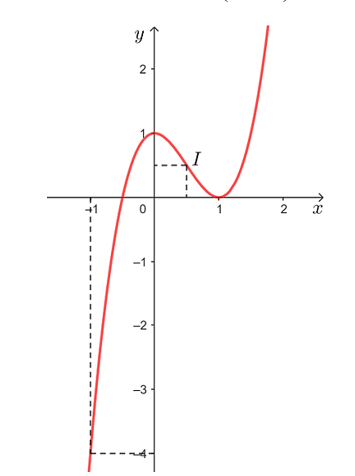
Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) y = 2x^3 – 3x^2 + 1; (ảnh 2)

Vậy đồ thị hàm số y = 2x³ – 3x² + 1 được cho như hình vẽ trên.

Tâm đối xứng của đồ thị hàm số đó là điểm I $(\frac{1}{2}; \frac{1}{2})$ .

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng.

Trong khoảng 50 giây đầu tiên kể từ khi đốt cháy các tên lửa hãm, độ cao h của con tàu so với bề mặt của Mặt Trăng được tính (gần đúng) bởi hàm

h(t) = – 0,01t³ + 1,1t² – 30t + 250,

trong đó t là thời gian tính bằng giây và h là độ cao tính bằng kilômét (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016).

a) Tìm thời điểm t (0 ≤ t ≤ 50) sao cho con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng. Khoảng cách nhỏ nhất này là bao nhiêu?

b) Vẽ đồ thị của hàm số y = h(t) với 0 ≤ t ≤ 70 (đơn vị trên trục hoành là 10 giây, đơn vị trên trục tung là 50 km).

Xem đáp án

Lời giải

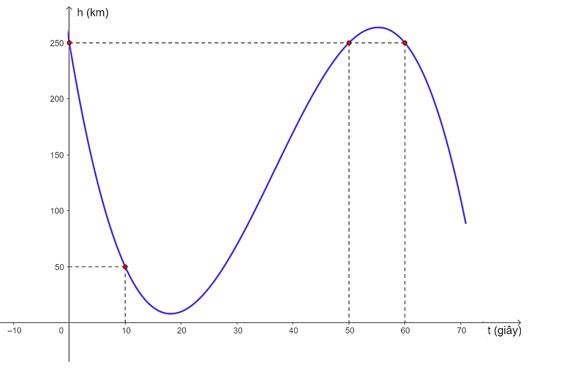
a) Xét hàm số h(t) = – 0,01t³ + 1,1t² – 30t + 250 với t ∈ [0; 50].

Ta có h'(t) = – 0,03t² + 2,2t – 30;

Trên khoảng (0; 50), h'(t) = 0 khi t ≈ 18.

h(0) = 250; h(18) = 8,08; h(50) = 250.

Do đó, $\min_{[0; 50]} h (t) = 8, 08$ tại t = 18.

Vậy tại thời điểm t = 18 giây thì con tàu đạt khoảng cách nhỏ nhất so với bề mặt của Mặt Trăng và khoảng cách nhỏ nhất này bằng 8,08 km.

b) Xét hàm số h(t) = – 0,01t³ + 1,1t² – 30t + 250 với t ∈ [0; 70].

Ta có h'(t) = – 0,03t² + 2,2t – 30;

Trên khoảng (0; 70), h'(t) = 0 khi t ≈ 18 hoặc t ≈ 55.

Bảng biến thiên của hàm số h(t) như sau:

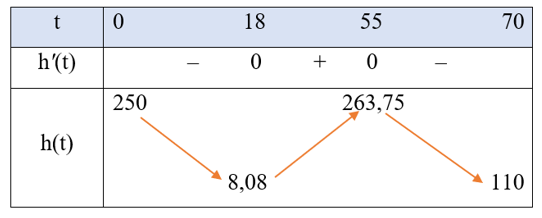
Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. (ảnh 1)

Trên khoảng (0; 70), đồ thị hàm số h(t) đi qua các điểm (0; 250), (10; 50), (50; 250) và (60; 250).

Một tàu đổ bộ tiếp cận Mặt Trăng theo cách tiếp cận thẳng đứng và đốt cháy các tên lửa hãm ở độ cao 250 km so với bề mặt của Mặt Trăng. (ảnh 2)

Câu 2

Lập bảng biến thiên và vẽ đồ thị của hàm số y = x² – 2x – 3.

Xem đáp án

Lời giải

Tập xác định của hàm số đã cho là ℝ.

Ta có y' = 2x – 2;

y' = 0 ⇔ 2x – 2 = 0 ⇔ x = 1.

Bảng biến thiên của hàm số như sau:

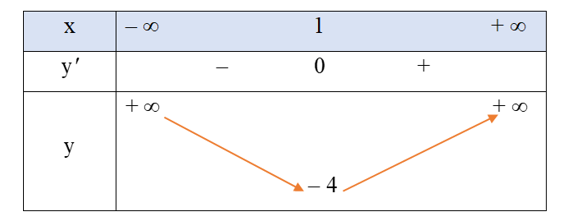
Lập bảng biến thiên và vẽ đồ thị của hàm số y = x^2 – 2x – 3. (ảnh 1)

Vẽ đồ thị hàm số:

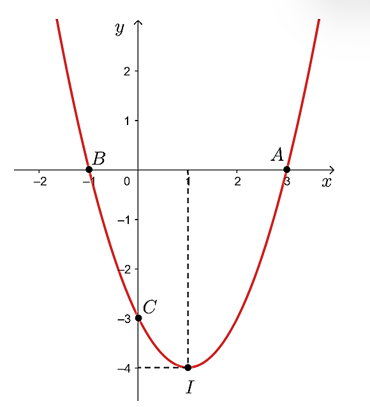
Hàm số y = x² – 2x – 3 là hàm số bậc hai nên đồ thị của nó là một parabol có:

+ Đỉnh I(1; – 4);

+ Giao với trục hoành tại các điểm A(3; 0) và B(– 1; 0);

+ Giao với trục tung tại điểm C(0; – 3).

Ta vẽ được đồ thị hàm số đã cho như sau:

Lập bảng biến thiên và vẽ đồ thị của hàm số y = x^2 – 2x – 3. (ảnh 2)

Câu 3

Trong 20 phút theo dõi, lưu lượng nước của một con sông được tính theo công thức

Q(t) = $- \frac{1}{5} t^{3} + 5 t^{2} + 100$ ,

trong đó Q được tính theo m³/phút, t tính theo phút, 0 ≤ t ≤ 20 (Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016). Khi lưu lượng nước của con sông lên đến 550 m³/phút thì cảnh báo lũ được đưa ra.

Trong thời gian theo dõi, lưu lượng nước của con sông lớn nhất là bao nhiêu? Cảnh báo lũ được đưa ra vào thời điểm nào?

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

b) y = x³ + 3x² + 3x + 1.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Xét phản ứng hóa học tạo ra chất C từ hai chất A và B:

A + B → C.

Giả sử nồng độ của hai chất A và B bằng nhau [A] = [B] = a (mol/l). Khi đó, nồng độ của chất C theo thời gian t (t > 0) được cho bởi công thức: [C] = $\frac{a^{2} K t}{a K t + 1}$ (mol/l), trong đó K là hằng số dương (Nguồn: Đỗ Đức Thái (Chủ biên) và các đồng tác giả, Giáo trình Phép tính vi tích phân hàm một biến, NXB Đại học Sư phạm, 2023).

a) Tìm tốc độ phản ứng ở thời điểm t > 0.

b) Chứng minh nếu x = [C] thì x'(t) = K(a – x)².

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Đường cong ở Hình 30 là đồ thị của hàm số:

A. $y = \frac{x^{2} + 2 x + 2}{- x - 1}$ .

B. $y = \frac{x^{2} + 2 x + 2}{x + 1}$ .

C. $y = \frac{x^{2} - 2 x + 2}{x - 1}$ .

D. $y = \frac{x^{2} - 2 x + 2}{x + 1}$ .

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau: a) y = 2x3 – 3x2 + 1;

Bình luận

Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 2x – 3.

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau: b) y = x3 + 3x2 + 3x + 1.

Đường cong ở Hình 30 là đồ thị của hàm số: A. y=x2+2x+2−x−1. B. y=x2+2x+2x+1. C. y=x2−2x+2x−1. D. y=x2−2x+2x+1.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) y = 2x³ – 3x² + 1;

Lập bảng biến thiên và vẽ đồ thị của hàm số y = x² – 2x – 3.

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

b) y = x³ + 3x² + 3x + 1.

Đường cong ở Hình 30 là đồ thị của hàm số:

A. $y = \frac{x^{2} + 2 x + 2}{- x - 1}$ .

B. $y = \frac{x^{2} + 2 x + 2}{x + 1}$ .

C. $y = \frac{x^{2} - 2 x + 2}{x - 1}$ .

D. $y = \frac{x^{2} - 2 x + 2}{x + 1}$ .