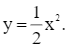Một cổng vòm được thiết kế dạng parabol y = ax2 như Hình 6.8. Biết chiều rộng của chân cổng là AB = 6 m và chiều cao của cổng là OI = 4,5 m.
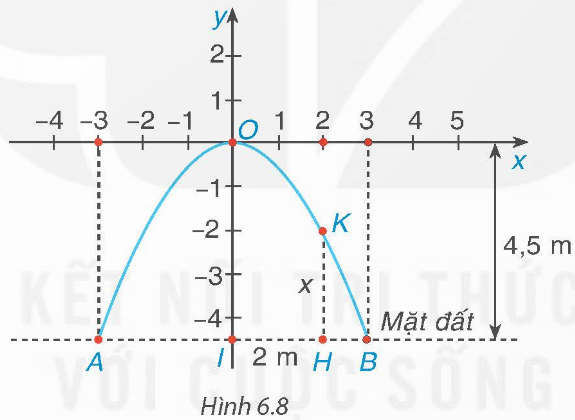
Để vận chuyển hàng qua cổng, người ta dự định sử dụng một xe tải có chiều rộng 2 m, chiều cao 3 m. Hỏi xe tải này có thể đi qua được cổng vòm đó hay không?
Một cổng vòm được thiết kế dạng parabol y = ax2 như Hình 6.8. Biết chiều rộng của chân cổng là AB = 6 m và chiều cao của cổng là OI = 4,5 m.

Quảng cáo
Trả lời:
Giả sử hình ảnh xe tải đi qua cổng có hình chữ nhật MNPQ có NP = 3 m và PQ = 2 m (hình vẽ).
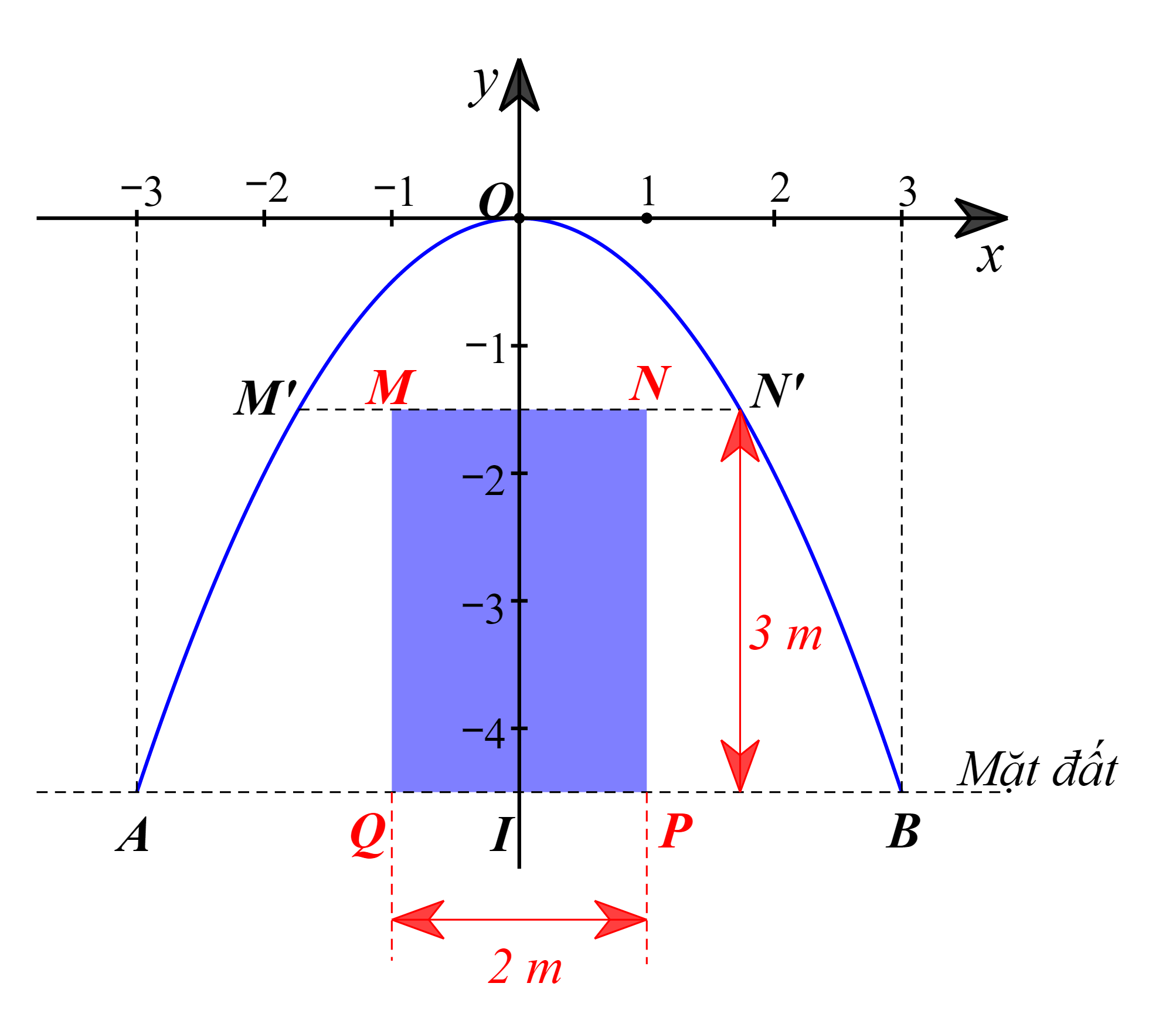
Xe tải có chiều cao NP = 3 m thì khi đó nó cách đỉnh vòm (gốc tọa độ O) một khoảng là 4,5 – 3 = 1,5 (m).
Khi y = –1,5, thay vào hàm số 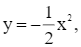 ta được:
ta được:
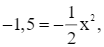 hay x2 = 3. Suy ra
hay x2 = 3. Suy ra ![]()
Khoảng cách giữa 2 điểm M’, N’ trên parabol lúc này là ![]()
Vậy xe tải có chiều rộng 2 m, chiều cao 3 m có thể đi qua được cổng vòm này.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
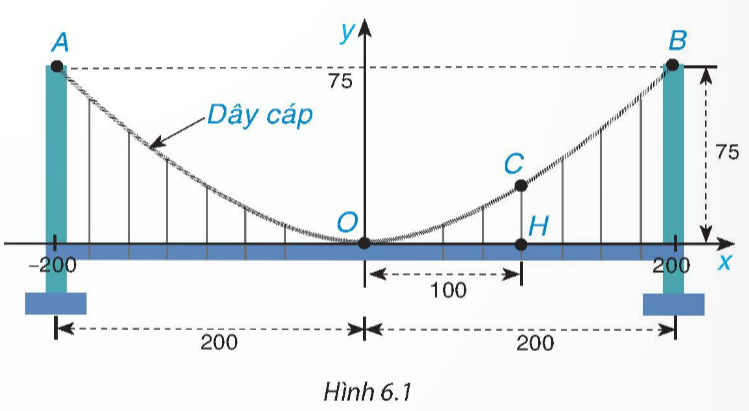
Sau bài học này, chúng ta sẽ giải quyết được câu hỏi trên như sau:
Vì các dây cáp có dạng đồ thị của hàm số y = ax2 (a ≠ 0) được treo trên các đỉnh tháp nên đồ thị hàm số y = ax2 (a ≠ 0) đi qua điểm B(200; 75).
Thay x = 200 và y = 75 vào hàm số y = ax2, ta được:
75 = a . 2002, hay 40 000a = 75, suy ra a = 0,001875 (thỏa mãn a ≠ 0).
Khi đó ta có hàm số y = 0,001875x2.
Chiều cao CH của dây cáp chính là tung độ của điểm C thuộc đồ thị hàm số y = 0,001875x2.
Thay hoành độ điểm C là x = 100 vào hàm số y = 0,001875x2, ta được:
y = 0,001875 . 1002 = 18,75.
Vậy chiều cao CH của dây cáp là 18,75 mét.
Lời giải
Lập bảng một số giá trị tương ứng giữa x và y:
|
x |
–2 |
–1 |
0 |
1 |
2 |
|
|
2 |
0,5 |
0 |
0,5 |
2 |
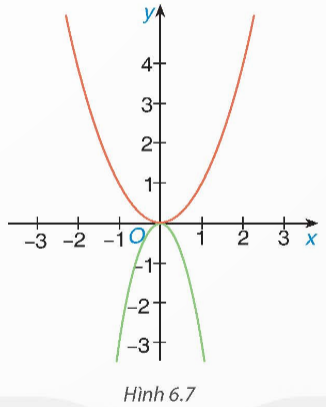
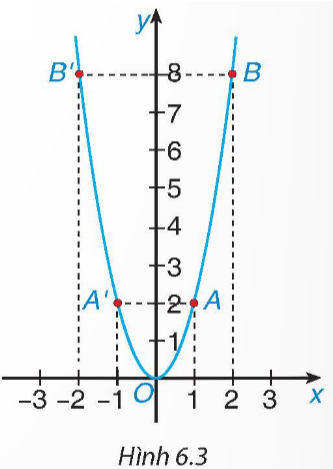
Biểu diễn các điểm (–2; 2); (–1; 0,5); (0; 0); (1; 0,5) và (2; 2) trên mặt phẳng tọa độ Oxy và nối chúng lại ta được đồ thị của hàm số 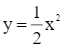 như hình vẽ dưới đây:
như hình vẽ dưới đây:
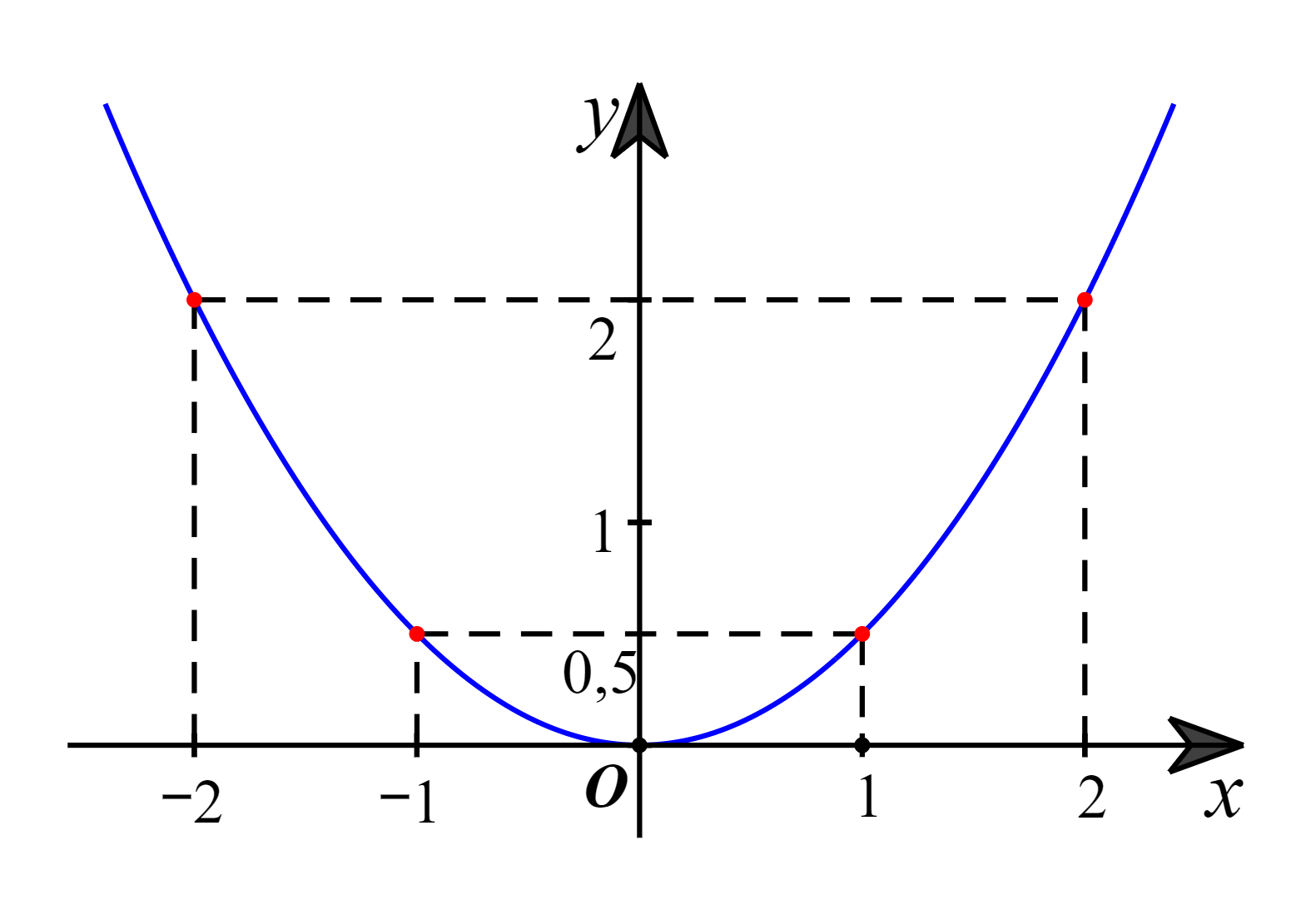
Ta có y = 2 nên 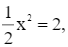 hay x2 = 4. Suy ra x = 2 hoặc x = –2.
hay x2 = 4. Suy ra x = 2 hoặc x = –2.
Vậy ta có hai điểm cần tìm là (–2; 2) và (2; 2). Hai điểm này đối xứng với nhau qua trục tung Oy.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.