Câu hỏi:
13/07/2024 2,548
Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức d = 0,05v2 + 1,1v để ước tính khoảng cách an toàn tối thiểu d (feet) (tức là độ dài quãng đường mà xe đi được kể từ khi đạp phanh đến khi xe dừng lại) đối với một phương tiện di chuyển với tốc độ v (dặm/giờ) (theo Algebra 2, NXB McGraw-Hill, 2008). Giả sử giới hạn tốc độ trên một đường cao tốc nào đó là 70 dặm/giờ. Nếu một ô tô có thể dừng lại sau 300 feet kể từ khi đạp phanh thì ô tô đó có chạy nhanh hơn giới hạn tốc độ của đường cao tốc này không?
Các kĩ sư đảm bảo an toàn của đường cao tốc thường sử dụng công thức d = 0,05v2 + 1,1v để ước tính khoảng cách an toàn tối thiểu d (feet) (tức là độ dài quãng đường mà xe đi được kể từ khi đạp phanh đến khi xe dừng lại) đối với một phương tiện di chuyển với tốc độ v (dặm/giờ) (theo Algebra 2, NXB McGraw-Hill, 2008). Giả sử giới hạn tốc độ trên một đường cao tốc nào đó là 70 dặm/giờ. Nếu một ô tô có thể dừng lại sau 300 feet kể từ khi đạp phanh thì ô tô đó có chạy nhanh hơn giới hạn tốc độ của đường cao tốc này không?
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài tập cuối chương 6 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ô tô có thể dừng lại sau 300 feet kể từ khi đạp phanh nên d = 300 (feet).
Thay d = 300 vào công thức d = 0,05v2 + 1,1v, ta được:
300 = 0,05v2 + 1,1v
0,05v2 + 1,1v – 300 = 0.
Ta có ∆ = 1,12 – 4.0,05.(–300) = 61,21 > 0.
Do đó, phương trình có hai nghiệm phân biệt:
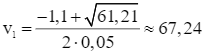(dặm/giờ) < 70 (dặm/giờ) (thỏa mãn);
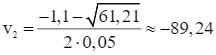(không thỏa mãn).
Vậy nếu ô tô có thể dừng lại sau 300 feet kể từ khi đạp phanh thì ô tô đó không chạy nhanh hơn giới hạn tốc độ của đường cao tốc này.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x là lãi suất năm của hình thức gửi tiết kiệm này (x viết dưới dạng số thập phân, x > 0).
Sau một năm, bác Hương nhận được số tiền cả vốn lẫn lãi là:
100 + 100x (triệu đồng).
Bác Hương gửi thêm 50 triệu đồng nên năm thứ hai bác gửi số tiền là:
100 + 100x + 50 = 150 + 100x (triệu đồng).
Đến cuối năm thứ hai bác Hương nhận được số tiền lãi là:
(150 + 100x).x (triệu đồng).
Sau hai năm (kể từ khi gửi lần đầu), số tiền bác Hương nhận được cả vốn lẫn lãi là:
150 + 100x + (150 + 100x).x = 150 + 250x + 100x2 (triệu đồng).
Theo bài, sau hai năm bác Hương nhận được số tiền cả vốn lẫn lãi là 176 triệu đồng nên ta có phương trình:
150 + 250x + 100x2 = 176
100x2 + 250x – 26 = 0
50x2 + 125x – 13 = 0.
Ta có ∆ = 1252 – 4.50.(–13) = 18 225 > 0 và 
Suy ra, phương trình trên có hai nghiệm phân biệt:
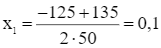(thỏa mãn); 
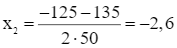(loại).
Vậy lãi suất năm của hình thức gửi tiết kiệm này là 0,1 = 10%.
Lời giải
Đổi 1 giờ 12 phút = 1,2 giờ.
Gọi thời gian học sinh khối lớp 9 làm riêng xong công việc là x (giờ) (x > 0).
Thời gian học sinh khối lớp 8 làm riêng xong công việc là x + 1 (giờ).
Một giờ khối lớp 9 làm được 
(công việc).
Một giờ khối lớp 8 làm được 
(công việc).
Một giờ cả hai khối làm được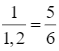 
(công việc).
Khi đó, ta có phương trình:
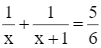
Quy đồng mẫu hai vế của phương trình, ta được:
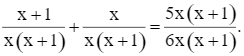
Nhân cả hai vế của phương trình với 6x(x + 1) để khử mẫu, ta được phương trình:
6(x + 1) + 6x = 5x(x + 1)
6x + 6 + 6x = 5x2 + 5x
5x2 – 7x – 6 = 0.
Ta có ∆ = (–7)2 – 4.5.(–6) = 169 và 
Suy ra, phương trình trên có hai nghiệm phân biệt:
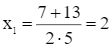(thỏa mãn); 
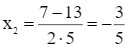(loại).
Vậy thời gian học sinh khối lớp 9 làm riêng xong công việc là 2 giờ, thời gian học sinh khối lớp 8 làm riêng xong công việc là 2 + 1 = 3 giờ.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
-
12 bài tập Một số bài toán thực tế liên quan đến bất đẳng thức có lời giải
-
Chuyên đề 8: Hình học (có đáp án)
-
12 bài tập Một số bài toán thực tế liên quan đến bất phương trình bậc nhất một ẩn có lời giải
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận