Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng ∆AXC ᔕ ∆DXB.
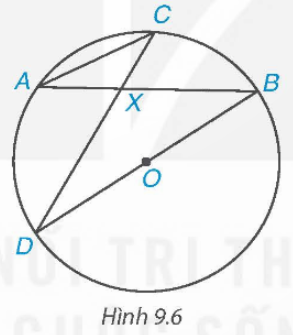
Cho đường tròn tâm O và hai dây cung AB, CD cắt nhau tại điểm X nằm trong đường tròn (H.9.6). Chứng minh rằng ∆AXC ᔕ ∆DXB.
Câu hỏi trong đề: Giải SGK Toán 9 KNTT Bài 27. Góc nội tiếp có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Xét đường tròn tâm O, có 
và 
là hai góc nội tiếp cùng chắn cung nhỏ AD
Suy ra 
hay 
Xét ∆AXC và ∆DXB có:
(hai góc đối đỉnh) và 
(chứng minh trên)
Do đó ∆AXC ᔕ ∆DXB (g.g).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
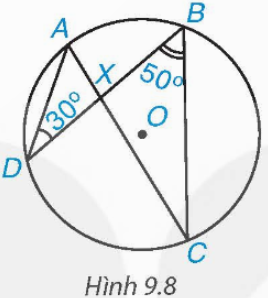
Xét đường tròn (O) có 
là hai góc nội tiếp cùng chắn cung nhỏ AB nên
Vì 
là góc ngoài của ∆BXC tại đỉnh X nên ta có:
Vậy 
Lời giải
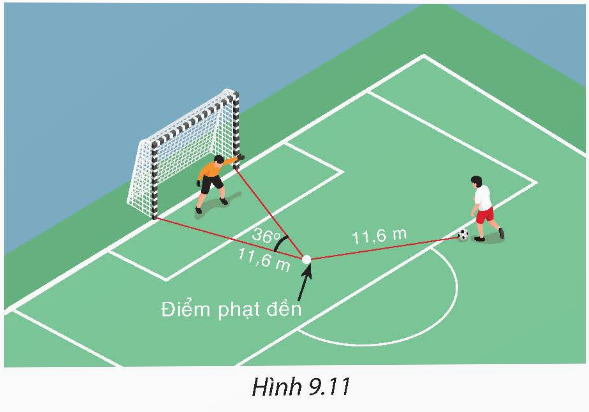
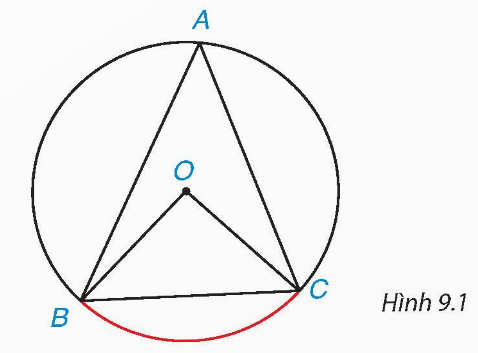
Hình vẽ dưới đây minh họa cho bài toán trên với A, B lần lượt là các cọc gôn, C là vị trí đặt bóng và O là vị trí điểm phạt đền.
Vì OA = OB = OC = 11,6 m nên A, B, C cùng thuộc đường tròn (O; 11,6 m).
Xét đường tròn (O; 11,6 m) có 
lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung nhỏ AB nên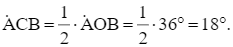 
Vậy khi quả bóng đặt ở vị trí cách điểm phạt đến 11,6 m thì góc sút bằng 18°.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo