Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) \(\int\limits_{\frac{\pi }{6}}^{\frac{\pi }{4}} {\frac{1}{{{{\sin }^2}x}}dx} = \left. { - \cot x} \right|_{\frac{\pi }{6}}^{\frac{\pi }{4}} = - 1 + \sqrt 3 \).
b) \(\int\limits_0^{\frac{\pi }{4}} {\left( {1 + \tan x} \right)\cos xdx} \)\( = \int\limits_0^{\frac{\pi }{4}} {\left( {\cos x + \sin x} \right)dx} \)\( = \int\limits_0^{\frac{\pi }{4}} {\cos xdx} + \int\limits_0^{\frac{\pi }{4}} {\sin xdx} \)
\( = \left. {\left( {\sin x - \cos x} \right)} \right|_0^{\frac{\pi }{4}}\)\( = 1\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
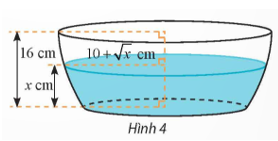
Diện tích của mặt cắt là: \(S\left( x \right) = \pi {\left( {10 + \sqrt x } \right)^2}\).
Dung tích của chậu là:
\(V = \int\limits_0^{16} {S\left( x \right)dx} = \pi \int\limits_0^{16} {{{\left( {10 + \sqrt x } \right)}^2}dx} \) \( = \pi \int\limits_0^{16} {\left( {100 + 20\sqrt x + x} \right)dx} \)
\( = \pi \left. {\left( {100x + \frac{{40}}{3}{x^{\frac{3}{2}}} + \frac{{{x^2}}}{2}} \right)} \right|_0^{16}\)\( = \frac{{7744}}{3}\pi \).
Lời giải
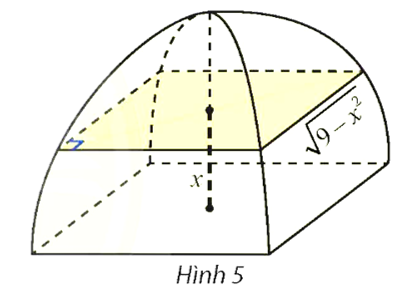
Diện tích mặt cắt là: \(S\left( x \right) = \left( {9 - {x^2}} \right)\) (m2).
Thể tích của lều là: \(V = \int\limits_0^3 {\left( {9 - {x^2}} \right)dx} \)\( = \left. {\left( {9x - \frac{{{x^3}}}{3}} \right)} \right|_0^3\)= 18.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
20 câu Trắc nghiệm Phương trình đường thẳng trong không gian có đáp án (Nhận biết)
Nhắn tin Zalo