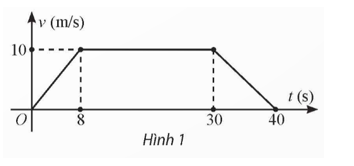
Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t) = 10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật.
a) Tính quãng đường s(t) vật di chuyển được sau thời gian t giây (trong khoảng thời gian vật đang rơi).
b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.
Sau khi được thả rơi tự do từ độ cao 100 m, một vật rơi xuống với tốc độ v(t) = 10t (m/s), trong đó t là thời gian tính theo giây kể từ khi thả vật.
a) Tính quãng đường s(t) vật di chuyển được sau thời gian t giây (trong khoảng thời gian vật đang rơi).
b) Sau bao nhiêu giây thì vật chạm đất? Tính tốc độ rơi trung bình của vật.
Câu hỏi trong đề: Giải SGK Toán 12 CTST Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Quãng đường s(t) vật di chuyển được sau thời gian t giây là:
\(s\left( t \right) = \int {v\left( t \right)dt} = \int {10tdt} = 5{t^2} + C\).
Vì s(0) = 0 nên C = 0.
Do đó s(t) = 5t2 .
b) Vật chạm đất khi s(t) = 100 Û 5t2 = 100 Þ \(t = 2\sqrt 5 \) (vì t > 0).
Vậy vật chạm đất sau \(2\sqrt 5 \approx 4,47\) giây.
Tốc độ rơi trung bình là \(\frac{1}{{2\sqrt 5 }}\int\limits_0^{2\sqrt 5 } {10tdt = } \frac{1}{{2\sqrt 5 }}.\left. {5{t^2}} \right|_0^{2\sqrt 5 } = 10\sqrt 5 \) m/s.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
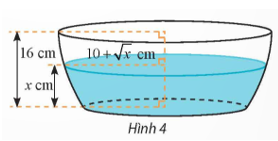
Diện tích của mặt cắt là: \(S\left( x \right) = \pi {\left( {10 + \sqrt x } \right)^2}\).
Dung tích của chậu là:
\(V = \int\limits_0^{16} {S\left( x \right)dx} = \pi \int\limits_0^{16} {{{\left( {10 + \sqrt x } \right)}^2}dx} \) \( = \pi \int\limits_0^{16} {\left( {100 + 20\sqrt x + x} \right)dx} \)
\( = \pi \left. {\left( {100x + \frac{{40}}{3}{x^{\frac{3}{2}}} + \frac{{{x^2}}}{2}} \right)} \right|_0^{16}\)\( = \frac{{7744}}{3}\pi \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
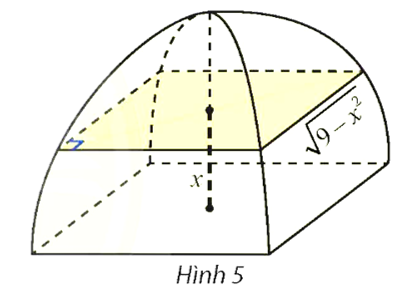
Diện tích mặt cắt là: \(S\left( x \right) = \left( {9 - {x^2}} \right)\) (m2).
Thể tích của lều là: \(V = \int\limits_0^3 {\left( {9 - {x^2}} \right)dx} \)\( = \left. {\left( {9x - \frac{{{x^3}}}{3}} \right)} \right|_0^3\)= 18.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập