Câu hỏi:
11/07/2024 923
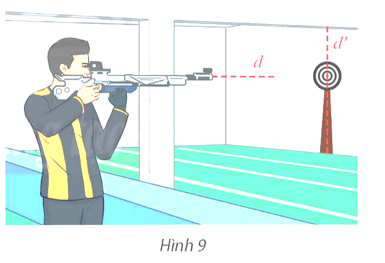
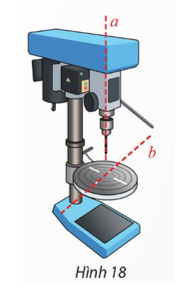
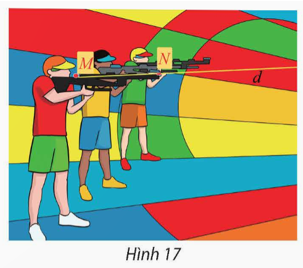
Cho hai đường thẳng d và d' có vectơ chỉ phương lần lượt là , .
a) Nhắc lại định nghĩa góc giữa hai đường thẳng d và d' trong không gian.
b) Vectơ \(\overrightarrow b = \left( { - 2; - 1; - 3} \right)\) có phải là một vectơ chỉ phương của d không?
c) Giải thích tại sao ta lại có đẳng thức cos(d, d') = \(\left| {\cos \left( {\overrightarrow a ,\overrightarrow {a'} } \right)} \right| = \left| {\cos \left( {\overrightarrow b ,\overrightarrow {a'} } \right)} \right|\).
d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Cho hai đường thẳng d và d' có vectơ chỉ phương lần lượt là , .
a) Nhắc lại định nghĩa góc giữa hai đường thẳng d và d' trong không gian.
b) Vectơ \(\overrightarrow b = \left( { - 2; - 1; - 3} \right)\) có phải là một vectơ chỉ phương của d không?
c) Giải thích tại sao ta lại có đẳng thức cos(d, d') = \(\left| {\cos \left( {\overrightarrow a ,\overrightarrow {a'} } \right)} \right| = \left| {\cos \left( {\overrightarrow b ,\overrightarrow {a'} } \right)} \right|\).
d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Góc giữa hai đường thẳng d và d' trong không gian, kí hiệu (d, d') là góc giữa hai đường thẳng a và b cùng đi qua một điểm và lần lượt song song hoặc trùng với d và d'.
b) \(\overrightarrow b = \left( { - 2; - 1; - 3} \right) = - \overrightarrow a \) . Do đó \(\overrightarrow b \) cũng là vectơ chỉ phương của đường thẳng d.
c) Vì \(\overrightarrow a ,\overrightarrow {a'} \) lần lượt là vectơ chỉ phương của hai đường thẳng d và d' nên:
+) (d, d') = \(\left( {\overrightarrow a ,\overrightarrow {a'} } \right)\) nếu \(0^\circ \le \left( {\overrightarrow a ,\overrightarrow {a'} } \right) \le 90^\circ \)
+) \(\left( {d,d'} \right) = 180^\circ - \left( {\overrightarrow a ,\overrightarrow {a'} } \right)\) nếu \(90^\circ < \left( {\overrightarrow a ,\overrightarrow {a'} } \right) \le 180^\circ \).
Do đó \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\overrightarrow a ,\overrightarrow {a'} } \right)} \right| = \left| {\cos \left( {\overrightarrow b ,\overrightarrow {a'} } \right)} \right|\).
d) \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\overrightarrow a ,\overrightarrow {a'} } \right)} \right| = \frac{{\left| {\overrightarrow a .\overrightarrow {a'} } \right|}}{{\left| {\overrightarrow a } \right|\left| {\overrightarrow {a'} } \right|}} = \frac{{\left| {2.3 + 1.2 + 3.\left( { - 8} \right)} \right|}}{{\sqrt {{2^2} + {1^2} + {3^2}} .\sqrt {{3^2} + {2^2} + {{\left( { - 8} \right)}^2}} }} = \frac{{16}}{{7\sqrt {22} }}\).
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đường thẳng d và d' lần lượt có vectơ chỉ phương là \(\overrightarrow a = \left( {1;0;0} \right),\overrightarrow {a'} = \left( {0;0;3} \right)\).
Ta có \(\overrightarrow a .\overrightarrow {a'} \) = 1.0 + 0.0 + 0.3 = 0.
Do đó d và d' vuông góc với nhau.
Lời giải
a) Đường thẳng a đi qua M(1; 2; 0) và có vectơ chỉ phương là \(\overrightarrow a = \left( {0;0;3} \right)\).
Đường thẳng b đi qua N(1; 2; 6) và có vectơ chỉ phương \(\overrightarrow {a'} = \left( {4;2;0} \right)\).
Có \(\overrightarrow a .\overrightarrow {a'} = 0.4 + 0.2 + 3.0 = 0\). Suy ra a ^ b.
Ta xét hệ \(\left\{ \begin{array}{l}1 = 1 + 4t'\\2 = 2 + 2t'\\3t = 6\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}t' = 0\\t' = 0\\t = 2\end{array} \right.\) . Suy ra hệ có nghiệm duy nhất.
Do đó a và b cắt nhau.
b) Thay t = 2 vào phương trình đường thẳng a ta được \(\left\{ \begin{array}{l}x = 1\\y = 2\\z = 6\end{array} \right.\).
Vậy tọa độ giao điểm của hai đường thẳng này là (1; 2; 6).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
-
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
-
79 câu Chuyên đề Toán 12 Bài 2 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
87 câu Chuyên đề Toán 12 Bài 3 Dạng 1: Xác định vectơ pháp tuyến và viết phương trình mặt phẳng có đáp án
-
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
-
56 câu Chuyên đề Toán 12 Bài 2: Lôgarit có đáp án
-
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
-
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận