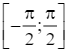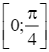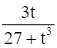Quảng cáo
Trả lời:
y = sin2x – x trên đoạn 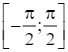 .
.
Tập xác định: D = ℝ.
Ta có: y = sin2x – x ⇒ y' = 2cos2x – 1.
y' = 0 ⇔ 2cos2x – 1 = 0 ⇔ x = ±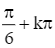 (k ∈ ℤ).
(k ∈ ℤ).
Xét trên khoảng 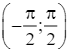 , y' = 0 khi x =
, y' = 0 khi x = ![]() hoặc x = −
hoặc x = −![]() .
.
Ta tính được: y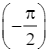 =
= ![]() , y
, y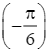 =
= 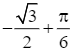 , y
, y![]() =
= 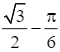 , y
, y![]() =
= ![]() .
.
Vậy ![]() y =
y = ![]() tại x =
tại x = ![]() ,
, ![]() y =
y = ![]() tại x =
tại x = ![]() .
.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
y = x + cos2x trên đoạn 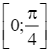 .
.
Tập xác định: D = ℝ.
Ta có: y = x + cos2x ⇒ y' = 1 – sin2x.
y' = 0 ⇔ x = ![]() (k ∈ ℤ).
(k ∈ ℤ).
Xét trên khoảng 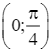 , ta thấy không có giá trị nào của x để y' = 0.
, ta thấy không có giá trị nào của x để y' = 0.
Ta tính được: y(0) = 1, y![]() =
= ![]() +
+ ![]() .
.
Vậy ![]() y =
y = ![]() +
+ ![]() tại x =
tại x = ![]() ,
, ![]() y = 1 tại x = 0.
y = 1 tại x = 0.
Lời giải
|
a) Đ |
b) Đ |
c) S |
d) Đ |
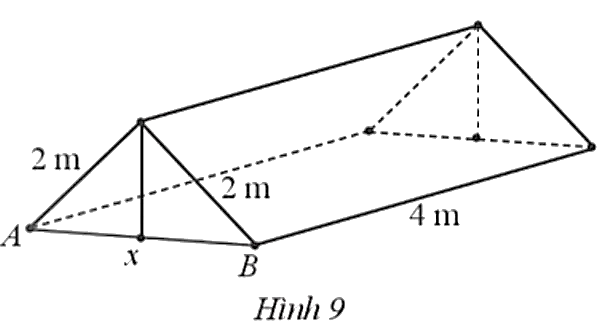
Thể tích của thùng chính bằng thể tích hình hộp nên V = x2. h (dm3).
Tổng diện tích xung quanh và diện tích 1 đáy của thùng (do thùng không nắp) là:
S = 4xh + x2 (dm2).
Theo đề, cái gò đựng đầy được 32 lít nước, tức là V = 32 (dm3).
⇒ x2. h = 32 ⇒ h = ![]() .
.
Khi đó S(x) = 4x.![]() + x2 =
+ x2 = ![]() .
.
Ta có: S(x) = ![]() ⇒ S'(x) =
⇒ S'(x) = ![]()
S'(x) = 0 ⇔ ![]() = 0 ⇔ x = 4.
= 0 ⇔ x = 4.
Ta có bảng biến thiên như sau:
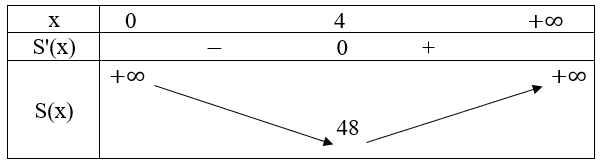
Vậy để làm được thùng mà tốn ít nguyên liệu nhất thì độ dài cạnh đáy của thùng là
4 dm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.