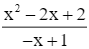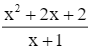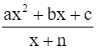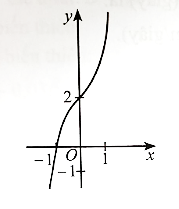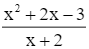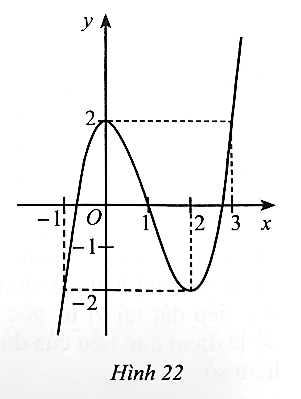Quảng cáo
Trả lời:
y = 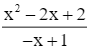
1) Tập xác định: D = ℝ\{1}.
2) Sự biến thiên.
Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.
Ta có: ![]() y = −∞,
y = −∞, ![]() y = +∞.
y = +∞.
![]() y = +∞,
y = +∞, ![]() y = −∞.
y = −∞.
Do đó, đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
![]()
![]() =
= ![]()
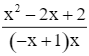 =
= ![]()
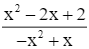 = −1.
= −1.
![]() [y – (−x)] =
[y – (−x)] = ![]()
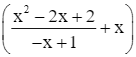 =
= ![]()
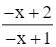 = 1.
= 1.
Do đó, đường thẳng y = −x + 1 là tiệm cận xiên của đồ thị hàm số.
Ta có: y' = 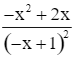
y' = 0 ⇔ 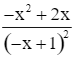 = 0 ⇔ x = 0 hoặc x = 2.
= 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên như sau:
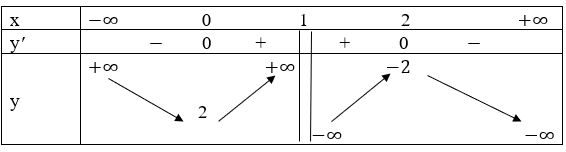
Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).
Hàm số đồng biến trên các khoảng (0; 1) và (1; 2).
Hàm số đạt cực tiểu tại x = 0, yCT = 2; hàm số đạt cực đại tại x = 2, yCĐ = −2.
3) Đồ thị
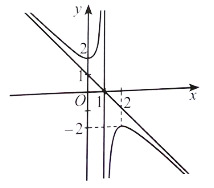
Đồ thị hàm số nhận đường thẳng x = 1 làm tiệm cận đứng và y = −x + 1 làm tiệm cận xiên.
Giao của đồ thị hàm số với trục tung là (0; 2).
Hàm số đi qua các điểm: 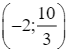 ;
; 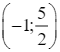 ; (0; 2); (2; −2);
; (0; 2); (2; −2); 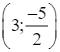 .
.
Ta có đồ thị hàm số:
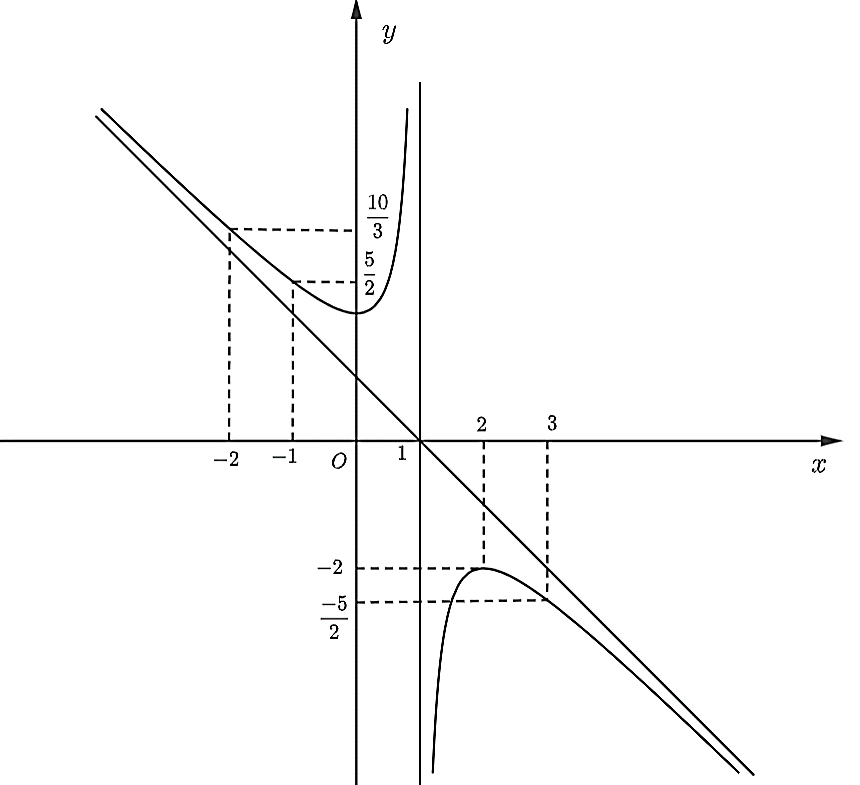
Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (1; 0) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
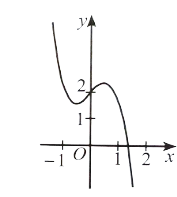
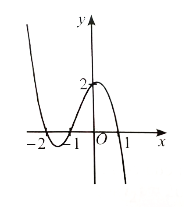
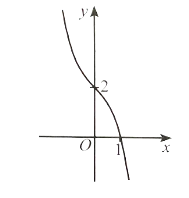
Đáp án đúng là: B
Ta có: y = 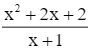
Tập xác định: D = ℝ\{−1}.
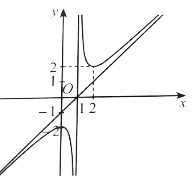
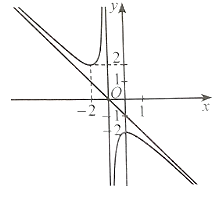
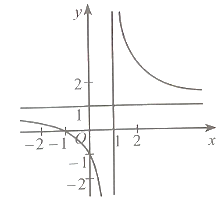
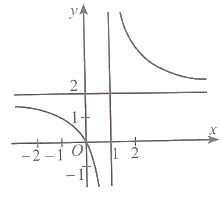
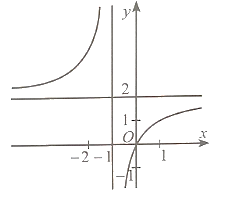
Đồ thị hàm số này có đường tiệm cận đứng x = −1 nên có thể là phương án B hoặc D.
Có hệ số của x2 ở tử là a = 1 và hệ số của x ở mẫu là m = 1 nên a, m cùng dấu.
Vậy phương án đúng là B.
Lời giải
|
a) S |
b) Đ |
c) Đ |
d) S |
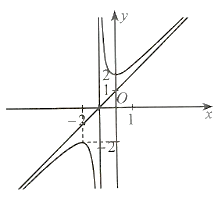
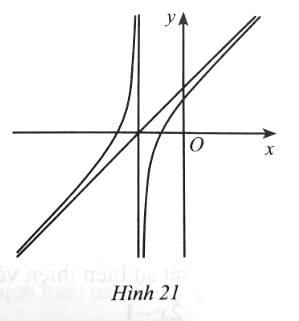
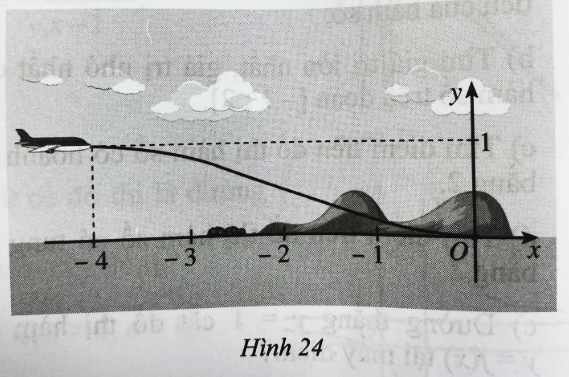
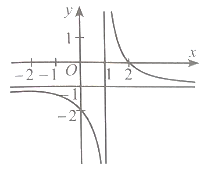
Tiệm cận đứng của đồ thị hàm số là đường thẳng x = −n nằm bên trái trục tung nên
−n < 0 hay n > 0.
Tiệm cận xiên có hệ số góc là a có hướng đi lên từ trái sang phải nên a > 0.
Đồ thị cắt trục tung tại điểm (0; ![]() ) nằm về phía trên trục hoành nên c > 0.
) nằm về phía trên trục hoành nên c > 0.
Đồ thị cắt trục hoành tại hai điểm có hoành độ âm nên phương trình ax2 + bx + c = 0 có hai nghiệm âm phân biệt nên ![]() < 0 hay b > 0.
< 0 hay b > 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.