1. Lớp 12
  2. Toán
  3. Giải SBT Toán 12 CD Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án

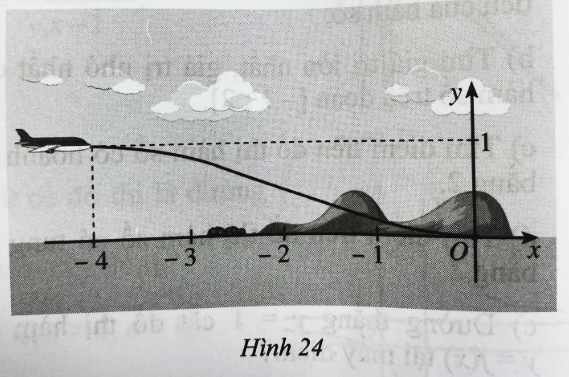
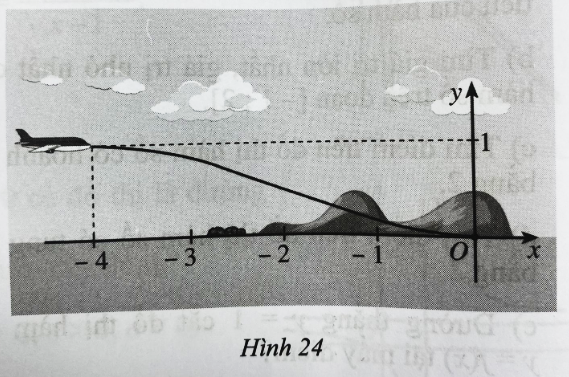
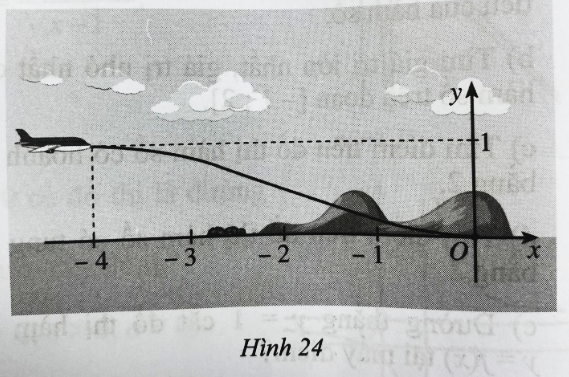
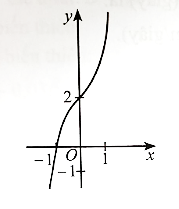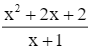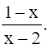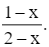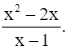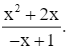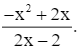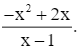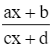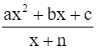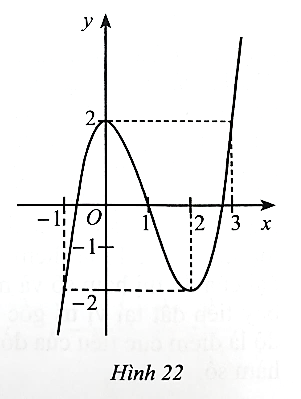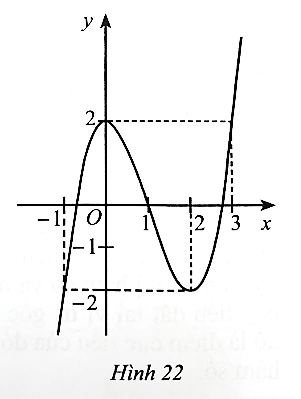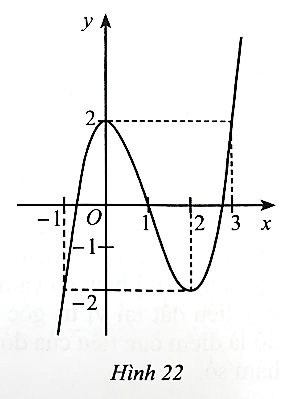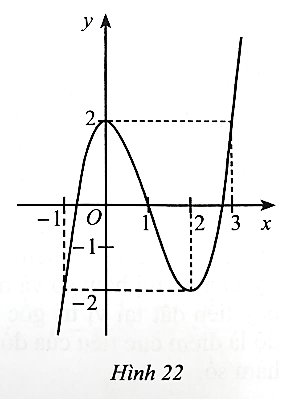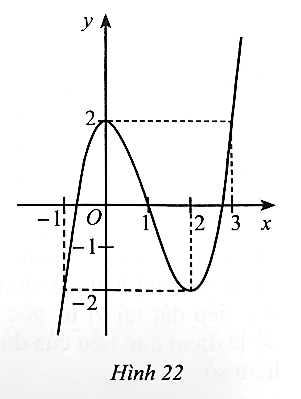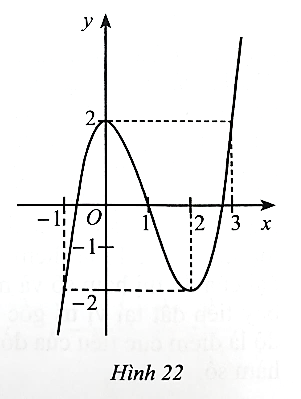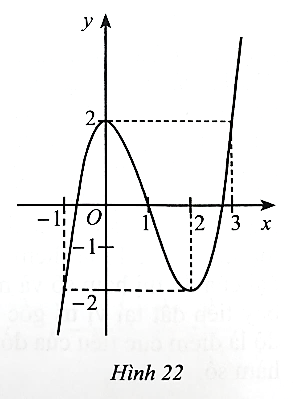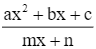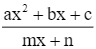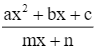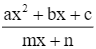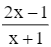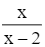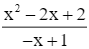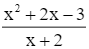Giải SBT Toán 12 CD Bài 4. Khảo sát sự biến thiên và vẽ đồ thị của hàm số có đáp án

30 người thi tuần này 4.6 728 lượt thi 32 câu hỏi

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

🔥 Học sinh cũng đã học

140 người thi tuần này

20000 câu trắc nghiệm tổng hợp Toán 2026 có đáp án - Phần 2

1 K lượt thi 95 câu hỏi
85 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Chương VI. Một số yếu tố xác suất

276 lượt thi 52 câu hỏi
44 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Chương V. Phương trình mặt phẳng, đường thẳng, mặt cầu trong không gian

235 lượt thi 73 câu hỏi
62 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm. Tích phân

253 lượt thi 91 câu hỏi
41 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Chương VI. Xác suất có điều kiện

206 lượt thi 52 câu hỏi
45 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Chương V. Phương trình mặt phẳng, đường thẳng, mặt cầu

210 lượt thi 88 câu hỏi
79 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm. Tích phân

244 lượt thi 76 câu hỏi
46 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương VI. Xác suất có điều kiện

361 lượt thi 52 câu hỏi

Danh sách câu hỏi:

Câu 1

Đồ thị hàm số y = 4x3 – 6x2 + 1 là đường cong nào trong các đường cong sau?

A.

B.

C.

D.

Lời giải

Đáp án đúng là: A

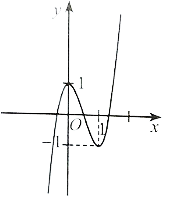
Do hệ số của x3 trong hàm số đã cho là a = 4 > 0 nên đồ thị hàm số có thể là phương án A hoặc C.

Mặt khác khi thay x = 1 vào hàm số y = 4x3 – 6x2 + 1 ta được y = −1 tức là đồ thị hàm số đi qua điểm có tọa độ (1; −1).

Vậy phương án đúng là A.

Câu 2

Đồ thị hàm số y = −x3 – x + 2 là đường cong nào trong các đường cong sau?

A.

B.

C.

D.

Lời giải

Đáp án đúng là: D

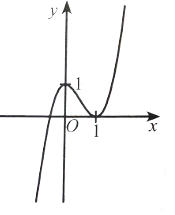
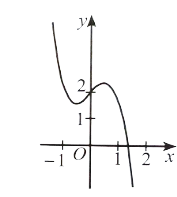
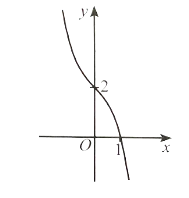
Do hệ số của x3 trong hàm số là a = −1 < 0 nên đồ thị hàm số có thể là phương án B hoặc D.

Mặt khác y' = −3x2 – 1 < 0 với ∀x nên đồ thị hàm số không có điểm cực trị.

Vậy phương án đúng là D.

Câu 3

Đồ thị hàm số y = là đường cong nào trong các đường cong sau?

A.

B.

C.

D.

Lời giải

Đáp án đúng là: D

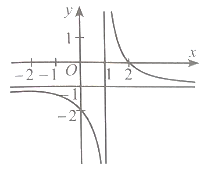
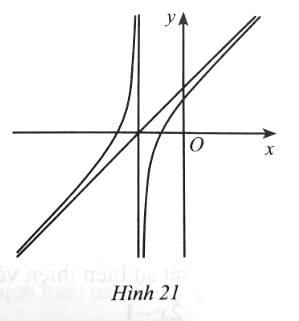
Ta có: y = .

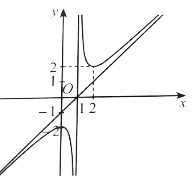
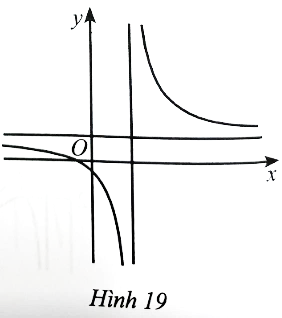
Tập xác định: D = ℝ\{−1}.

Có y' = 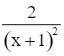> 0 với ∀x ∈ D.

Hàm số đồng biến trên mỗi khoảng (−∞; −1) và (−1; +∞) nên trên mỗi khoảng này đồ thị hàm số đi lên từ trái qua phải, do đó phương án đúng là D.

Câu 4

Đồ thị hàm số y = là đường cong nào trong các đường cong sau?

A.

B.

C.

D.

Lời giải

Đáp án đúng là: B

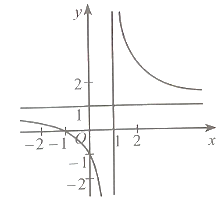
Ta có: y =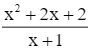

Tập xác định: D = ℝ\{−1}.

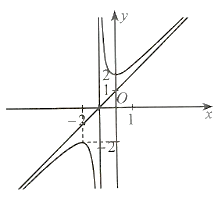
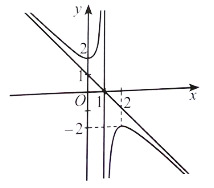
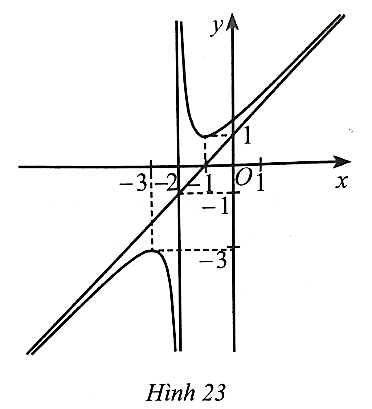
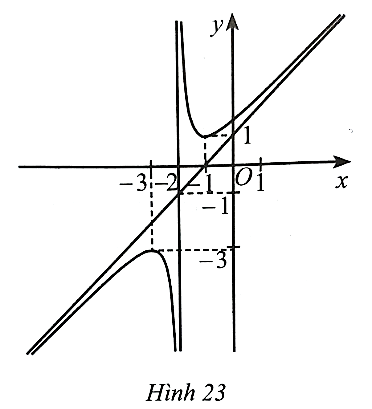
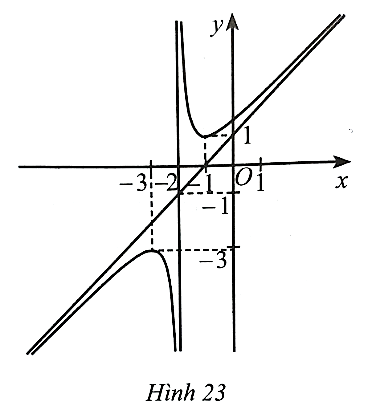
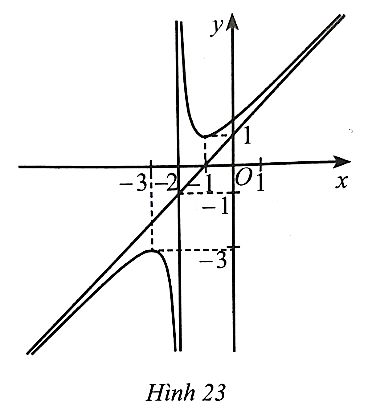
Đồ thị hàm số này có đường tiệm cận đứng x = −1 nên có thể là phương án B hoặc D.

Có hệ số của x2 ở tử là a = 1 và hệ số của x ở mẫu là m = 1 nên a, m cùng dấu.

Vậy phương án đúng là B.

Câu 5

Đường cong ở Hình 16 là đồ thị của hàm số:

A. y = + x2 – 4.

B. y = x3 – 3x2 – 4.

C. y = x3 + 3x2 – 4.

D. y = −x3 – 3x2 + 4.

Lời giải

Đáp án đúng là: C

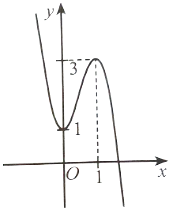
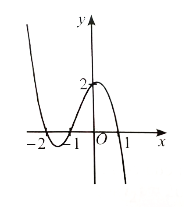
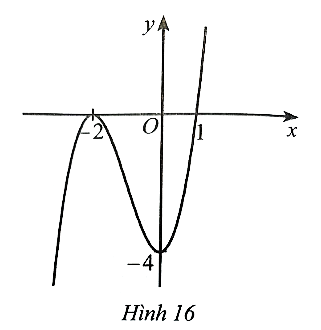
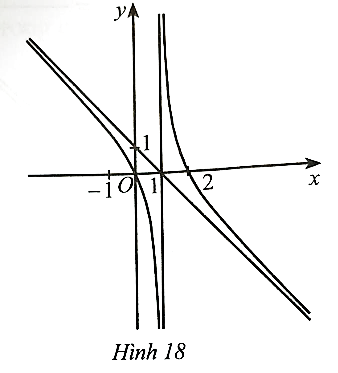
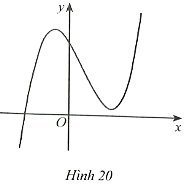
Dựa vào đồ thị hàm số ở Hình 16, ta có:

Hệ số a > 0 nên phương án có thể là B hoặc C.

Đồ thị hàm số đi qua điểm (−2; 0).

Khi thay x = −2 vào phương án B được y = (−2)3 – 3.(−2)2 – 4 = −24 ≠ 0 nên phương án B loại.

Vậy phương án đúng là C.

Câu 6

Đường cong ở Hình 17 là đồ thị của hàm số:

A. y =

B. y =

C. y =

D. y =

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Đường cong ở Hình 18 là đồ thị của hàm số:

A. y =

B. y =

C. y =

D. y =

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Cho hàm số y = với a > 0 có đồ thị là đường cong ở Hình 19. Mệnh đề nào dưới đây là đúng?

A. b > 0, c < 0, d < 0.

B. b > 0, c > 0, d < 0.

C. b < 0, c > 0, d < 0.

D. b < 0, c < 0, d < 0.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Cho hàm số y = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là đường cong ở Hình 20.

a) a > 0.

Đ

S

b) Đồ thị cắt trục tung tại điểm có tung độ dương.

Đ

S

c) Đồ thị hàm số có hai điểm cực trị nằm cùng phía với trục tung.

Đ

S

d) b < 0.

Đ

S

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Cho hàm số y = có đồ thị là đường cong ở Hình 21.

a) n < 0.

Đ

S

b) a > 0.

Đ

S

c) c > 0.

Đ

S

d) b < 0.

Đ

S

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn [−1; 2].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Tìm điểm trên đồ thị hàm số có hoành độ bằng 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Tìm điểm trên đồ thị hàm số có tung độ bằng 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Đường thẳng y = 1 cắt đồ thị hàm số y = f(x) tại mấy điểm?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Với giá trị nào của x thì −2 < f(x) < 2.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho hàm số bậc ba y = f(x) = ax3 + bx2 + cx + d có đồ thị là đường cong như Hình 22.

Căn cứ vào đồ thị hàm số:

Tìm công thức xác định hàm số f(x).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Cho hàm số y = f(x) = với (a, m ≠ 0) có đồ thị là đường cong như Hình 23.

Căn cứ vào đồ thị hàm số:

 Tìm khoảng đơn điệu, điểm cực đại, cực tiểu của hàm số.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Cho hàm số y = f(x) = với (a, m ≠ 0) có đồ thị là đường cong như Hình 23.

Căn cứ vào đồ thị hàm số:

Viết phương trình đường tiệm cận đứng, tiệm cận xiên của đồ thị hàm số.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Cho hàm số y = f(x) = với (a, m ≠ 0) có đồ thị là đường cong như Hình 23.

Căn cứ vào đồ thị hàm số:

Phương trình f(x) = 3 có bao nhiêu nghiệm?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho hàm số y = f(x) = với (a, m ≠ 0) có đồ thị là đường cong như Hình 23.

Căn cứ vào đồ thị hàm số:

Tìm công thức xác định hàm số y = f(x), biết m = 1.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
y = (x – 2)(x + 1)2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

y = x3 – x2 + 2;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
y = 2x3 – 3x2 + 2x – 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

y = (x3 – 6x2 + 12x).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

 y = ;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

y = ;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

y = ;

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:
y = .

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gắn với hệ trục tọa độ Oxy với mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có tọa độ (−4; 1) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm số.

a) Tìm công thức xác định hàm số mô phỏng đường bay của máy bay trên đoạn [−4; 0].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gắn với hệ trục tọa độ Oxy với mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có tọa độ (−4; 1) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm số.

Khi máy bay cách vị trí hạ cánh theo phương ngang 3 dặm thì máy bay bay cách mặt đất bao nhiêu dặm? (Biết đơn vị trên hệ trục tọa độ là dặm).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Một máy bay loại nhỏ bắt đầu hạ cánh, đường bay của nó gắn với hệ trục tọa độ Oxy với mô phỏng ở Hình 24. Biết đường bay của nó có dạng đồ thị hàm số bậc ba; vị trí bắt đầu hạ cánh có tọa độ (−4; 1) là điểm cực đại của đồ thị hàm số và máy bay tiếp đất tại vị trí gốc tọa độ là điểm cực tiểu của đồ thị hàm số.

Khi ở độ cao 0,5 dặm, máy bay cách vị trí hạ cánh theo phương ngang bao nhiêu dặm?

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đăng ký

Bạn đã có tài khoản?

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập