Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN như hình bên. Chứng minh rằng SP vuông góc với AB.
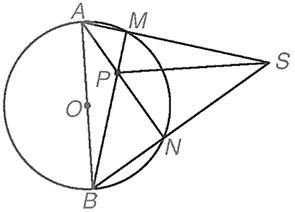
Cho đường tròn (O), đường kính AB và điểm S nằm ngoài (O). Cho hai đường thẳng SA, SB lần lượt cắt (O) tại M (khác A) và N (khác B). Gọi P là giao điểm của BM và AN như hình bên. Chứng minh rằng SP vuông góc với AB.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài 27. Góc nội tiếp có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(\widehat {AMB} = \widehat {ANB} = \frac{1}{2}\widehat {AOB} = 90^\circ .\) Do vậy BM ⊥ SA, AN ⊥ SB. Suy ra P là trực tâm của tam giác SAB. Do đó SP ⊥ AB.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
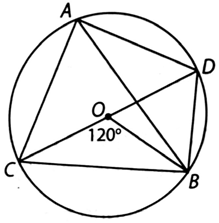
a) Xét đường tròn (O), ta có:
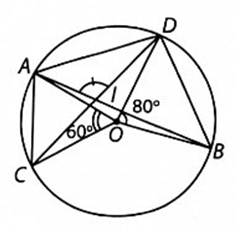
− Góc nội tiếp ADC và góc ở tâm AOC cùng chắn một cung nên \[\widehat {ADC} = \frac{{\widehat {AOC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ ;\]
− Góc nội tiếp BAD và góc ở tâm BOD cùng chắn một cung nên \(\widehat {BAD} = \frac{{\widehat {BOD}}}{2} = \frac{{80^\circ }}{2} = 40^\circ .\)
Do tổng ba góc trong một tam giác bằng 180° nên:
\(\widehat {AID} = 180^\circ - \widehat {BAD} - \widehat {ADC} = 180^\circ - 40^\circ - 30^\circ = 110^\circ .\)
b) Hai tam giác IAC và IDB có:
\[\widehat {AIC} = \widehat {DIB}\] (hai góc đối đỉnh),
\(\widehat {CAI} = \widehat {CAB} = \widehat {CDB} = \widehat {IDB}\) (vì \(\widehat {CAB}\) và \(\widehat {CDB}\) là hai góc nội tiếp của (O) cùng chắn cung ).
Suy ra ∆IAC ᔕ ∆IDB (g.g). Do đó \(\frac{{IA}}{{ID}} = \frac{{IC}}{{IB}},\) hay IA.IB = IC.ID.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
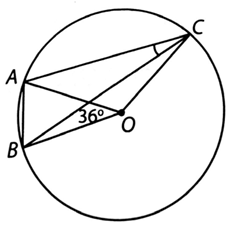
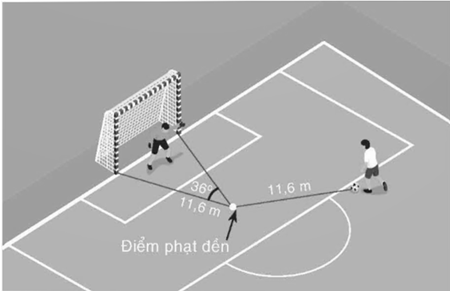
Gọi O là vị trí phạt đền, vị trí hai cọc gôn lần lượt là A, B và vị trí quả bóng là C.
Khi đó A, B, C cùng nằm trên đường tròn (O) với bán kính 11,6 m.
Khi đó \(\widehat {ACB}\) và \(\widehat {AOB}\) lần lượt là góc nội tiếp và góc ở tâm của (O) cùng chắn cung AB. Do đó \(\widehat {ACB} = \frac{{\widehat {AOB}}}{2} = \frac{{36^\circ }}{2} = 18^\circ .\)
Vậy góc sút khi trái bóng ở vị trí cách điểm phạt đền 11,6 m là 18°.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập