Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Chứng minh rằng AH = 2OM.
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC và M là trung điểm của BC. Chứng minh rằng AH = 2OM.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài tập cuối chương 9 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
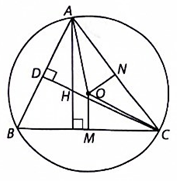
Kẻ đường cao CD của tam giác ABC. Gọi N là trung điểm của cạnh AC.
Khi đó tam giác AOC cân tại O nên ON cũng là đường phân giác của góc AOC.
Do vậy \[\widehat {AON} = \frac{{\widehat {AOC}}}{2} = \widehat {ABC}.\]
Suy ra \(\widehat {NAO} = 90^\circ - \widehat {AON} = 90^\circ - \widehat {ABC} = \widehat {DAH}.\)
Tương tự \[\widehat {MCO} = 90^\circ - \widehat {COM} = 90^\circ - \widehat {DAC} = \widehat {DCA}.\]
Hai tam giác NAO và DAH có:
\(\widehat {NAO} = \widehat {DAH}\) (chứng minh trên), \(\widehat {ANO} = \widehat {ADH} = 90^\circ .\)
Do đó ∆NAO ᔕ ∆DAH (g.g).
Suy ra \(\frac{{AO}}{{AH}} = \frac{{AN}}{{AD}},\) hay \(AH = \frac{{AO.AD}}{{AN}} = \frac{{2AO.AD}}{{AC}}.\) (1)
Hai tam giác OMC và ADC có:
\[\widehat {MCO} = \widehat {DCA}\] (chứng minh trên), \[\widehat {OMC} = \widehat {ADC} = 90^\circ .\]
Vì vậy ∆OMC ᔕ ∆ADC (g.g).
Suy ra \(\frac{{OM}}{{AD}} = \frac{{OC}}{{AC}}.\)
Do đó \(2OM = \frac{{2OC.AD}}{{AC}} = \frac{{2OA.OC}}{{AC}} = AH\) (theo (1)).
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
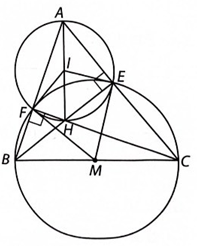
a) Do hai tam giác AEH và AFH vuông tại E và F nên IE = IA = IH = IF.
Vì vậy tứ giác AEHF nội tiếp đường tròn (I, IA).
b) Tương tự như trên, tứ giác BCEF có \(\widehat {BFC} = \widehat {BEC} = 90^\circ \) nên tứ giác BCEF nội tiếp đường tròn (M, MB).
Suy ra \[\widehat {AEF} = 180^\circ - \widehat {{\rm{CEF}}} = \widehat {FBC} = \widehat {ABC}.\]
Vì ∆IFA cân tại I nên \(\widehat {IFA} = \widehat {IAF} = \widehat {HAB} = 90^\circ - \widehat {ABC}.\) (1)
Mặt khác, ta có MF = MC, hay ∆MFC cân tại M. Suy ra \(\widehat {MFC} = \widehat {MCF}.\) (2)
Vì vậy ta có:
\(\widehat {MFI} = \widehat {MFC} + \widehat {CFI} = \widehat {MCF} + \left( {90^\circ - \widehat {IFA}} \right) = \left( {90^\circ - \widehat {ABC}} \right) + \widehat {ABC} - 90^\circ \) (theo (1) và (2)).
Do đó MF ⊥ IF. Suy ra MF tiếp xúc với (I, IA). Tương tự MR tiếp xúc với (I, IA).
Lời giải
Hình vuông cạnh 3 cm có đường chéo bằng: \(\sqrt {{3^2} + {3^2}} = 3\sqrt 2 \) (cm).
Đường tròn ngoại tiếp hình vuông này có bán kính: \(R = \frac{{3\sqrt 2 }}{2}\) (cm).
Vậy lục giác đều có cạnh: \(a = R = \frac{{3\sqrt 2 }}{2}\) (cm).
Chu vi của lục giác đều là: \(\mathcal{C} = 6.\frac{{3\sqrt 2 }}{2} = 9\sqrt 2 \) (cm).
Lục giác đều là hợp của 6 tam giác đều cạnh a, chiều cao \(h = \frac{{\sqrt 3 }}{2}a = \frac{{\sqrt 3 }}{2}.\frac{{3\sqrt 2 }}{2} = \frac{{3\sqrt 6 }}{4}\,\,(cm)\) nên có diện tích là:
\(S = 6.\frac{{ah}}{2} = 6.\frac{{\frac{{3\sqrt 2 }}{2}.\frac{{3\sqrt 6 }}{4}}}{2} = \frac{{27\sqrt 3 }}{4}\) (cm2).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo