Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm.
a) Tính độ dài đường cao OH của tam giác AOB.
b) Chứng minh đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Tính độ dài các đoạn thẳng AH và BH.
Cho hình thoi ABCD có O là giao điểm hai đường chéo, OA = 6 cm, OB = 8 cm.
a) Tính độ dài đường cao OH của tam giác AOB.
b) Chứng minh đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Tính độ dài các đoạn thẳng AH và BH.
Quảng cáo
Trả lời:
Giải bởi Vietjack
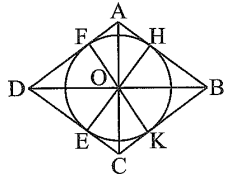
a) Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc nhau.
Áp dụng định lí Pythagore vào ∆AOB vuông tại O, ta có:
\[AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{6^2} + {8^2}} = \sqrt {36 + 64} = \sqrt {100} = 10\,\,{\rm{(cm}}).\]
Ta có \[{S_{\Delta OAB}} = \frac{1}{2} \cdot OA \cdot OB = \frac{1}{2} \cdot OH \cdot AB\]
Suy ra OA.OB = OH.AB
Do đó \(OH = \frac{{OA \cdot OB}}{{AB}} = \frac{{6 \cdot 8}}{{10}} = 4,8\;(\;{\rm{cm}}).\)
b) Lần lượt vẽ các đường cao OK, OE, OF của tam giác BOC, COD, DOA.
Ta có bốn tam giác vuông AOB, AOD, COD, COB bằng nhau (c.g.c), suy ra bốn đường cao OH, OF, OE, OK cũng bằng nhau. Do khoảng cách từ O đến bốn cạnh của hình thoi đều bằng OH nên đường tròn (O; OH) tiếp xúc với các cạnh của hình thoi.
c) Xét tam giác OAB vuông tại O có: \(\cos \widehat {OAH} = \frac{{OA}}{{AB}}.\)
Xét tam giác OAH vuông tại H có:
\(AH = OA \cdot \cos \widehat {OAB} = OA \cdot \frac{{OA}}{{AB}} = \frac{{O{A^2}}}{{AB}} = \frac{{{6^2}}}{{10}} = 3,6\;(\;{\rm{cm}}).\)
Do đó BH = AB – AH = 10 – 3,6 = 6,4 (cm).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
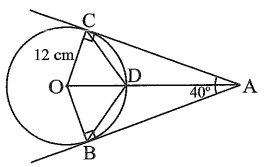
a) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AO là tia phân giác của \(\widehat {BAC},\) suy ra \(\widehat {OAC} = \frac{{\widehat {BAC}}}{2} = 20^\circ .\)
Xét ∆OAC vuông tại C có \(\widehat {AOC} + \widehat {OAC} = 90^\circ \)
Suy ra \(\widehat {AOC} = 90^\circ - \widehat {OAC} = 90^\circ - 20^\circ = 70^\circ \) hay \[\widehat {DOC} = 70^\circ .\]
Xét ∆ODC cân tại O (do OC = OD), có \(\widehat {ODC} = \frac{{180^\circ - \widehat {COD}}}{2} = \frac{{180^\circ - 70^\circ }}{2} = 55^\circ .\)
b) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AC = AB.
Xét ∆OAC vuông tại C ta có:
⦁ \(AC = OC \cdot \tan \widehat {AOC} = 12 \cdot \tan 70^\circ \approx 33\;(\;{\rm{cm}}).\)
Do đó AC = AB ≈ 33 cm.
⦁ \(OC = OA \cdot \sin \widehat {OAC}\)
Suy ra \(OA = \frac{{OC}}{{\sin \widehat {OAC}}} = \frac{{12}}{{\sin 20^\circ }} \approx 35\;(\;{\rm{cm}}).\)
Lời giải
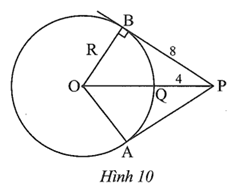
Do PB và PA là hai tiếp tuyến của đường tròn (O) lần lượt tại B và A
Suy ra OB ⊥ BP; OA ⊥ AP
Nên ∆OBP vuông tại B; ∆OAP vuông tại A.
Xét ∆OPB vuông tại B, ta có OP2 = OB2 + PB2 (định lí Pythagore)
Hay (OQ + QP)2 = OB2 + PB2
Suy ra (R + 4)2 = R2 + 82
R2 + 8R + 16 = R2 + 64
8R = 48
R = 6.
Do đó OP = OQ + QP = 6 + 4 = 10.
Như vậy, \(\sin \widehat {BOP} = \frac{{PB}}{{OP}} = \frac{8}{{10}} = \frac{4}{5},\) suy ra \(\widehat {BOP} \approx 53^\circ .\)
Theo bài, hai tiếp tuyến AP và BP của đường tròn (O; R) cắt nhau tại P nên OP là tia phân giác của góc AOB.
Khi đó, \(\widehat {AOB} = 2\widehat {BOP} \approx 2 \cdot 53^\circ = 106^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo