Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilômét? Biết rằng bán kính Trái Đất là khoảng 6 400 km. Làm tròn kết quả đến hàng phần trăm.
Một người ngồi trên trạm quan sát cao 15 m so với mực nước biển. Vào ngày trời trong xanh thì tầm nhìn xa tối đa của người đó là bao nhiêu kilômét? Biết rằng bán kính Trái Đất là khoảng 6 400 km. Làm tròn kết quả đến hàng phần trăm.
Quảng cáo
Trả lời:
Giải bởi Vietjack
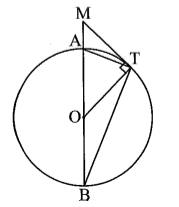
Theo đề bài ta có hình vẽ trên. Trong đó điểm M biểu diễn vị trí của người ngồi trên trạm quan sát, điểm A biểu diễn vị trí của trạm quan sát, điểm T biểu diễn điểm xa nhất mà người đó nhìn thấy. Khi đó đoạn thẳng MT là tầm nhìn xa tối đa từ M.
Vì T là điểm nhìn xa tối đa nên MT là tiếp tuyến của đường tròn (đường tròn coi như là bề mặt Trái Đất). Đặt h = MA = 15 m = 0,015 km, R = OA = OT = 6 400 km.
Áp dụng định lí Pythagore cho tam giác OTM vuông tại T, ta có:
MT2 = OM2 – OT2 = (h + R)2 – R2 = h2 + 2Rh
Suy ra \(MT = \sqrt {{h^2} + 2Rh} = \sqrt {0,{{015}^2} + 2 \cdot 6\,\,400 \cdot 0,015} \approx 13,86\;(\;{\rm{km}}).\)
Vậy tầm nhìn xa tối đa của người đó là khoảng 13,86 km.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
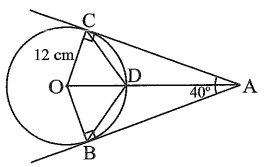
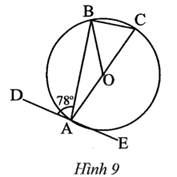
a) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AO là tia phân giác của \(\widehat {BAC},\) suy ra \(\widehat {OAC} = \frac{{\widehat {BAC}}}{2} = 20^\circ .\)
Xét ∆OAC vuông tại C có \(\widehat {AOC} + \widehat {OAC} = 90^\circ \)
Suy ra \(\widehat {AOC} = 90^\circ - \widehat {OAC} = 90^\circ - 20^\circ = 70^\circ \) hay \[\widehat {DOC} = 70^\circ .\]
Xét ∆ODC cân tại O (do OC = OD), có \(\widehat {ODC} = \frac{{180^\circ - \widehat {COD}}}{2} = \frac{{180^\circ - 70^\circ }}{2} = 55^\circ .\)
b) Ta có hai tiếp tuyến tại B và C của đường tròn (O) cắt nhau tại A nên AC = AB.
Xét ∆OAC vuông tại C ta có:
⦁ \(AC = OC \cdot \tan \widehat {AOC} = 12 \cdot \tan 70^\circ \approx 33\;(\;{\rm{cm}}).\)
Do đó AC = AB ≈ 33 cm.
⦁ \(OC = OA \cdot \sin \widehat {OAC}\)
Suy ra \(OA = \frac{{OC}}{{\sin \widehat {OAC}}} = \frac{{12}}{{\sin 20^\circ }} \approx 35\;(\;{\rm{cm}}).\)
Lời giải
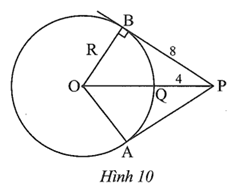
Do PB và PA là hai tiếp tuyến của đường tròn (O) lần lượt tại B và A
Suy ra OB ⊥ BP; OA ⊥ AP
Nên ∆OBP vuông tại B; ∆OAP vuông tại A.
Xét ∆OPB vuông tại B, ta có OP2 = OB2 + PB2 (định lí Pythagore)
Hay (OQ + QP)2 = OB2 + PB2
Suy ra (R + 4)2 = R2 + 82
R2 + 8R + 16 = R2 + 64
8R = 48
R = 6.
Do đó OP = OQ + QP = 6 + 4 = 10.
Như vậy, \(\sin \widehat {BOP} = \frac{{PB}}{{OP}} = \frac{8}{{10}} = \frac{4}{5},\) suy ra \(\widehat {BOP} \approx 53^\circ .\)
Theo bài, hai tiếp tuyến AP và BP của đường tròn (O; R) cắt nhau tại P nên OP là tia phân giác của góc AOB.
Khi đó, \(\widehat {AOB} = 2\widehat {BOP} \approx 2 \cdot 53^\circ = 106^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo