Cho parabol \(\left( P \right):y = \frac{1}{2}{x^2}\) và đường thẳng \(\left( a \right):y = - mx + 3\) (với \(m\) là tham số).
1) Vẽ parabol \(\left( P \right)\).
2) Tìm tất cả giá trị của tham số \(m\) để \(\left( d \right)\) thỏa mãn cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \[{x_1},\,\,{x_2}\] thỏa mãn \({x_1}\left( {x_2^2 - 6} \right) = 24\).
Cho parabol \(\left( P \right):y = \frac{1}{2}{x^2}\) và đường thẳng \(\left( a \right):y = - mx + 3\) (với \(m\) là tham số).
1) Vẽ parabol \(\left( P \right)\).
2) Tìm tất cả giá trị của tham số \(m\) để \(\left( d \right)\) thỏa mãn cắt \(\left( P \right)\) tại hai điểm phân biệt có hoành độ \[{x_1},\,\,{x_2}\] thỏa mãn \({x_1}\left( {x_2^2 - 6} \right) = 24\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
\(x\) |
\( - 2\) |
\( - 1\) |
0 |
1 |
2 |
|
\(y = \frac{1}{2}{x^2}\) |
2 |
\(\frac{1}{2}\) |
0 |
\(\frac{1}{2}\) |
2 |
Đồ thị hàm số là đường cong parabol đi qua các điểm \(O\left( {0\,;\,\,0} \right);\,\,A\left( { - 2\,;\,\,2} \right);\,\,B\left( { - 1;\,\,\frac{1}{2}} \right);\)\(C\left( {1;\,\,\frac{1}{2}} \right);\,\,D\left( {2;\,\,2} \right).\)
Hệ số \(a = \frac{1}{2} > 0\) nên parabol có bề cong hướng lên, đồ thị hàm số nhận \[Oy\] làm trục đối xứng.
Ta vẽ được đồ thị hàm số \(y = \frac{1}{2}{x^2}\) như sau:
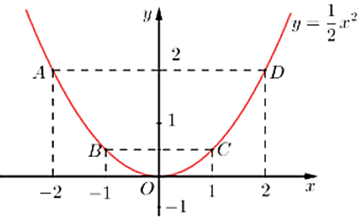
2) Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right)\), ta có:
\(\frac{1}{2}{x^2} = - mx + 3\) hay \(\frac{1}{2}{x^2} + mx - 3 = 0.\)
Xét \(\Delta = {m^2} - 4 \cdot \frac{1}{2} \cdot \left( { - 3} \right) = {m^2} + 6 > 0\) nên phương trình có hai nghiệm phân biệt.
Áp dụng định lí Viète, ta có: \(\left\{ {\begin{array}{*{20}{l}}{{x_1} + {x_2} = \frac{{ - m}}{{\frac{1}{2}}} = - 2m}\\{{x_1} \cdot {x_2} = \frac{{ - 3}}{{\frac{1}{2}}} = - 6}\end{array}} \right.\).
Khi đó \({x_1}\left( {x_2^2 - 6} \right) = 24\) hay \({x_1}\left( {x_2^2 + {x_1}{x_2}} \right) = 24\) nên \({x_1}{x_2}\left( {{x_2} + {x_1}} \right) = 24\)
Suy ra \( - 6 \cdot \left( { - 2m} \right) = 24\), suy ra \(12m = 24\) hay \(m = 2\).
Vậy \(m = 2\) thỏa mãn yêu cầu bài toán.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Gọi số học sinh dự kiến là \(x\) (học sinh). Điều kiện \(x \in \mathbb{N}*,\,\,x > 2.\)
Dự kiến mỗi học sinh chuyển số phần quà là: \(\frac{{120}}{x}\) (phần quà).
Thực tế số học sinh là: \(x - 2\) (học sinh).
Thực tế mỗi học sinh chuyển số phần quà là: \(\frac{{120}}{{x - 2}}\) (phần quà).
Vì thực tế mỗi học sinh phải chuyển nhiều hơn so với dự kiến 2 phần quà nên ta có phương trình \(\frac{{120}}{x} + 2 = \frac{{120}}{{x - 2}}\)
\[120\left( {x - 2} \right) + 2x\left( {x - 2} \right) = 120x\]
\[120x - 240 + 2{x^2} - 4x = 120x\]
\[{x^2} - 2x - 120 = 0\]
\(x = 12\) (thỏa mãn điều kiện) hoặc \(x = - 10\) (không thỏa mãn điều kiện).
Vậy dự kiến có 12 học sinh.
2) Ta có \(\sqrt {x + 4} + \sqrt {1 - 2x} = 3\) (điều kiện \( - 4 \le x \le \frac{1}{2}\,).\)
\(x + 4 + 1 - 2x + 2\sqrt {\left( {x + 4} \right)\left( {1 - 2x} \right)} = 9\)
\(2\sqrt {\left( {x + 4} \right)\left( {1 - 2x} \right)} - \left( {x + 4} \right) = 0\)
\(\sqrt {x + 4} \left( {2\sqrt {1 - 2x} - \sqrt {x + 4} } \right) = 0\)
\(\sqrt {x + 4} = 0\) hoặc \(2\sqrt {1 - 2x} = \sqrt {x + 4} \)
\(x + 4 = 0\) hoặc \(4\left( {1 - 2x} \right) = x + 4\)
\(x = - 4\) hoặc \(4 - 8x = x + 4\)
\(x = - 4\) (thỏa mãn) hoặc \(x = 0\) (thỏa mãn).
Vậy phương trình đã cho có nghiệm \(x = - 4\) và \(x = 0\).
Lời giải
Ta có \(P = x\left( {\sqrt {12 - 3{x^2}} + 1 - {x^2}} \right) = x\sqrt {12 - 3{x^2}} + x - {x^3}\).
Áp dụng bất đẳng thức Cauchy, ta có:
\(x\sqrt {12 - 3{x^2}} = \frac{{2 \cdot 3x\sqrt {12 - 3{x^2}} }}{6} \le \frac{{9{x^2} + 12 - 3{x^2}}}{6} = {x^2} + 2\).
Suy ra \[P \le {x^2} + 2 + x - {x^3} = - {\left( {x - 1} \right)^2}\left( {x + 1} \right) + 3 \le 3\].
Dấu xảy ra khi và chỉ khi \(x = 1\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập