Tìm giá trị lớn nhất của biểu thức: \(P = x\left( {\sqrt {12 - 3{x^2}} + 1 - {x^2}} \right)\), với \(x\) là số thực thỏa mãn \(0 \le x \le 2\).
Tìm giá trị lớn nhất của biểu thức: \(P = x\left( {\sqrt {12 - 3{x^2}} + 1 - {x^2}} \right)\), với \(x\) là số thực thỏa mãn \(0 \le x \le 2\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có \(P = x\left( {\sqrt {12 - 3{x^2}} + 1 - {x^2}} \right) = x\sqrt {12 - 3{x^2}} + x - {x^3}\).
Áp dụng bất đẳng thức Cauchy, ta có:
\(x\sqrt {12 - 3{x^2}} = \frac{{2 \cdot 3x\sqrt {12 - 3{x^2}} }}{6} \le \frac{{9{x^2} + 12 - 3{x^2}}}{6} = {x^2} + 2\).
Suy ra \[P \le {x^2} + 2 + x - {x^3} = - {\left( {x - 1} \right)^2}\left( {x + 1} \right) + 3 \le 3\].
Dấu xảy ra khi và chỉ khi \(x = 1\).
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
1) Gọi số học sinh dự kiến là \(x\) (học sinh). Điều kiện \(x \in \mathbb{N}*,\,\,x > 2.\)
Dự kiến mỗi học sinh chuyển số phần quà là: \(\frac{{120}}{x}\) (phần quà).
Thực tế số học sinh là: \(x - 2\) (học sinh).
Thực tế mỗi học sinh chuyển số phần quà là: \(\frac{{120}}{{x - 2}}\) (phần quà).
Vì thực tế mỗi học sinh phải chuyển nhiều hơn so với dự kiến 2 phần quà nên ta có phương trình \(\frac{{120}}{x} + 2 = \frac{{120}}{{x - 2}}\)
\[120\left( {x - 2} \right) + 2x\left( {x - 2} \right) = 120x\]
\[120x - 240 + 2{x^2} - 4x = 120x\]
\[{x^2} - 2x - 120 = 0\]
\(x = 12\) (thỏa mãn điều kiện) hoặc \(x = - 10\) (không thỏa mãn điều kiện).
Vậy dự kiến có 12 học sinh.
2) Ta có \(\sqrt {x + 4} + \sqrt {1 - 2x} = 3\) (điều kiện \( - 4 \le x \le \frac{1}{2}\,).\)
\(x + 4 + 1 - 2x + 2\sqrt {\left( {x + 4} \right)\left( {1 - 2x} \right)} = 9\)
\(2\sqrt {\left( {x + 4} \right)\left( {1 - 2x} \right)} - \left( {x + 4} \right) = 0\)
\(\sqrt {x + 4} \left( {2\sqrt {1 - 2x} - \sqrt {x + 4} } \right) = 0\)
\(\sqrt {x + 4} = 0\) hoặc \(2\sqrt {1 - 2x} = \sqrt {x + 4} \)
\(x + 4 = 0\) hoặc \(4\left( {1 - 2x} \right) = x + 4\)
\(x = - 4\) hoặc \(4 - 8x = x + 4\)
\(x = - 4\) (thỏa mãn) hoặc \(x = 0\) (thỏa mãn).
Vậy phương trình đã cho có nghiệm \(x = - 4\) và \(x = 0\).
Lời giải
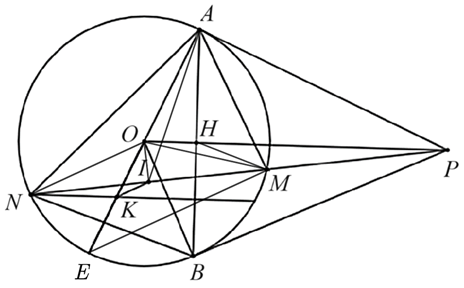
1) Do \[PA,{\rm{ }}PB\] là tiếp tuyến nên \(\widehat {OAP} = \widehat {OBP} = 90^\circ .\)
Xét tứ giác \[PAOB\] có
\(\widehat {OAP} + \widehat {OBP} = 90^\circ + 90^\circ = 180^\circ \).
Mà \(\widehat {OAP},\,\,\widehat {OBP}\) ở vị trí đối diện nên tứ giác \[PAOB\] nội tiếp.
2) Ta có \(PA = PB\) (tính chất hai tiếp tuyến cắt nhau), \(OA = OB = R\) nên \(PO\) là trung trực của \[AB.\]
Suy ra \(PO \bot AB\) tại \(H\) là trung điểm của \[AB.\]
Xét \(\Delta PAH\) và \(\Delta PAH\)\(\Delta POA\) có \[\widehat {PHA} = \widehat {PAO} = 90^\circ ;\] \(\widehat {APH}\) chung.
Do đó .
Suy ra \[\frac{{PA}}{{PH}} = \frac{{PO}}{{PA}}\] hay \(P{A^2} = PH \cdot PO\) (đpcm).
3) Xét \(\Delta PBM\) và \(\Delta PNB\) có \(\widehat {BPM}\) chung và
Do đó suy ra \[\frac{{PB}}{{PN}} = \frac{{PM}}{{PB}}\] hay \[P{B^2} = PM \cdot PN = P{A^2}\].
Mà \(P{A^2} = PH \cdot PO\) nên \(PM \cdot PN = PH \cdot PO\) hay\(\frac{{PM}}{{PO}} = \frac{{PH}}{{PN}}\).
Xét \(\Delta PMH\) và \(\Delta PON\) có \(\widehat {OPN}\) chung; \(\frac{{PM}}{{PO}} = \frac{{PH}}{{PN}}\) (cmt).
Do đó , suy ra \(\widehat {PMH} = \widehat {PON}\) (hai góc tương ứng).
Mặt khác \(\widehat {PMH} + \widehat {NMH} = 180^\circ \) (kề bù) nên \(\widehat {PON} + \widehat {NMH} = 180^\circ \).
Mà \(\widehat {PON},\,\,\widehat {NMH}\) nằm ở vị trí đối diện nên tứ giác \(HMNO\) nội tiếp.
Suy ra \(\widehat {OMN} = \widehat {OHN}\) (cùng chắn cung \[ON\,)\].
4) Kẻ đường kính \[AE\] của \(\left( O \right)\). Do \[I\] là trung điểm của \[MN\] nên \(OI \bot MN.\)
Xét tam giác \(OMN\,\,\left( {OM = ON} \right)\) có \(OI\) là đường trung tuyến (vì \[I\] là trung điểm của \[MN)\]nên \(OI\) cũng là đường cao hay \(OI \bot MN.\)
Suy ra \[\widehat {OIP} + \widehat {OAP} = 90^\circ + 90^\circ = 180^\circ \].
Mà \[\widehat {OIP},\,\,\widehat {OAP}\] nằm ở trị trí đối diện nên tứ giác \(OIPA\) nội tiếp.
Suy ra \[\widehat {IPO} = \widehat {IAO}\] (cùng chắn cung \[IO\,)\]
Mà \(\widehat {IPO} = \widehat {INK}\) (\[OP\,{\rm{//}}\,NK\], so le trong) nên \(\widehat {IAO} = \widehat {INK}\).
Chứng minh bổ đề: Cho tứ giác \(ABCD\) có \(\widehat {ACB} = \widehat {ADB}.\) Chứng minh tứ giác \(ABCD\) là tứ giác nội tiếp.
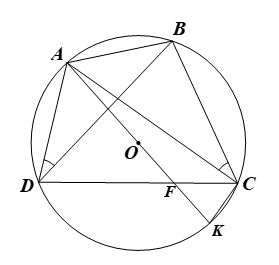
• Giả sử \(\Delta ABC\) có đường tròn ngoại tiếp tâm \(O\) và đường kính \(AK\) nên tứ giác \(ABCK\) nội tiếp, suy ra \(\widehat {ACB} = \widehat {AKB}\) (hai góc nội tiếp cùng chắn cung \(AB).\)
Mà \(\widehat {ACB} = \widehat {ADB}\) (giả thiết) nên \(\widehat {ADB} = \widehat {AKB}.\) \(\left( 6 \right)\)
⦁ Gọi \(F\) là giao điểm của \(AK\) và \(BD,\) \(F\) nằm trong đường tròn \(\left( O \right).\)
Xét \(\Delta AFD\) và \(\Delta BFK\) có: \(\widehat {AFD} = \widehat {BFK}\) (đối đỉnh) và \(\widehat {ADF} = \widehat {BKF}\) (chứng minh trên)
Do đó suy ra \(\frac{{AF}}{{BF}} = \frac{{DF}}{{KF}}\) nên \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}.\)
Xét \(\Delta DFK\) và \(\Delta AFB\) có: \(\frac{{AF}}{{DF}} = \frac{{BF}}{{KF}}\) và \[\widehat {DFK} = \widehat {AFB}\] (đối đỉnh)
Do đó suy ra \(\widehat {FDK} = \widehat {FAB}.\,\,\,\left( 7 \right)\)
⦁ Ta có \(\widehat {ABK}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ABK} = 90^\circ ,\) do đó \(\Delta ABK\) vuông tại \(B,\) suy ra \(\widehat {FAB} + \widehat {AKB} = 90^\circ .\,\,\,\left( 8 \right)\)
Từ \(\left( 6 \right),\,\,\left( 7 \right),\,\,\left( 8 \right)\) suy ra \(\widehat {ADB} + \widehat {FDK} = 90^\circ \) hay \(\widehat {ADK} = 90^\circ .\)
Khi đó \(\Delta ADK\) vuông tại \(D\) nên điểm \(D\) nằm trên đường tròn đường kính \(AK.\)
Suy ra tứ giác \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) đường kính \(AK.\)
Áp dụng bổ đề trên cho tứ giác \(IKNA\) có \(\widehat {IAO} = \widehat {INK}\) nên tứ giác \(IKNA\) nội tiếp.
Suy ra \[\widehat {NIK} = \widehat {NAK}\] (cùng chắn cung \[NK\]).
Mà \(\widehat {NAK} = \widehat {NME}\) (cùng chắn cung \[NE\]) nên \[\widehat {NIK} = \widehat {NME}\] suy ra \[IK\,{\rm{//}}\,ME\] (hai góc đồng vị bằng nhau)
Mặt khác \(\widehat {AME} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn) nên \(ME \bot AM.\)
Do đó \(NK \bot AM\) (đpcm).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo