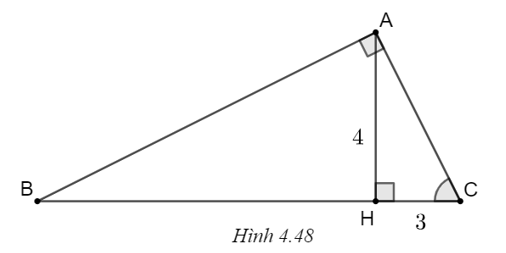
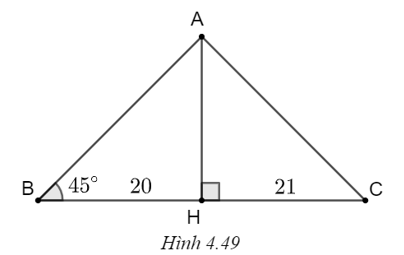
Cho tam giác ABC vuông tại A có \(\widehat B = 60^\circ ,\) BC = 20 cm.
a) Tính AB, AC.
b) Kẻ đường cao AH của tam giác. Tính AH, HB, HC.
Cho tam giác ABC vuông tại A có \(\widehat B = 60^\circ ,\) BC = 20 cm.
a) Tính AB, AC.
b) Kẻ đường cao AH của tam giác. Tính AH, HB, HC.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
(H.4.39)
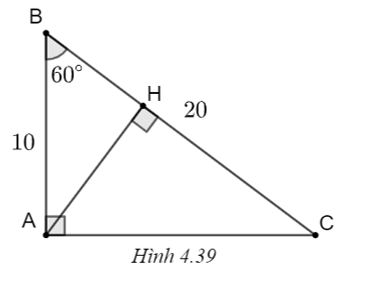
a) Trong tam giác ABC vuông tại A, ta có
\(AB = BC.\cos B = 20.\cos 60^\circ = 20.\frac{1}{2} = 10\) (cm);
\(AC = BC.\sin B = 20.\frac{{\sqrt 3 }}{2} = 10\sqrt 3 \) (cm).
b) Trong tam giác AHC vuông tại H, ta có
\(AH = AB.\sin B = 10.\sin 60^\circ = 10.\frac{{\sqrt 3 }}{2} = 5\sqrt 3 \) (cm);
\(BH = AB.\cos 60^\circ = 10.\frac{1}{2} = 5\) (cm).
Do đó CH = BC – BH = 20 – 5 = 15 (cm).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
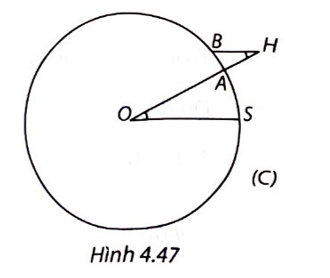
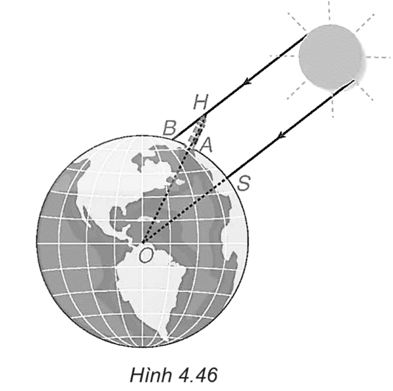
Trên Hình 4.47 đường tròn (C) với tâm O là tâm Trái Đất, đi qua S (Syene), A (Alexandria), OS = OA = R (R là bán kính của đường tròn (C)).
Theo giả thiết, cung tròn (nhỏ) SA của (C) dài 800 km.
Gọi H là đỉnh tháp, chân tại A thì A nằm giữa O và H, AH = 25 m. Bóng của tháp là cung tròn AB của (C).
Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}.\)
Vì AH = 25 m khá bé so với R, Erastosthene coi cung tròn AB của (C) là một đoạn thẳng AB = 3,1 m vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có
\(\tan \widehat {AHB} = \frac{{AB}}{{AH}} = \frac{{3,1}}{{25}} = 0,124.\)
Suy ra \(\tan \widehat {{\rm{AOS}}} = 0,124\) nên \(\widehat {AOS} \approx 7^\circ .\)
Vì độ dài cung tròn MN tùy ý trên đường tròn tâm O tỉ lệ thuận với số đo góc ở tâm \(\widehat {MON},\) mà độ dài cung AS bằng 800 km ứng với góc ở tâm \(\widehat {AOS} \approx 7^\circ \) nên toàn bộ đường tròn (C) ứng với góc ở tâm 360° có độ dài xấp xỉ bằng
\(\frac{{360^\circ }}{{7^\circ }}.800 \approx 41142\) (km).
Vậy chu vi của Trái Đất xấp xỉ 41142 km.
Lời giải
(H.4.45)
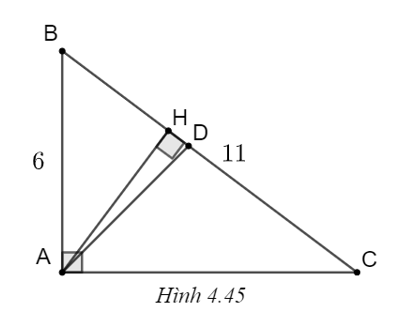
a) Trong tam giác vuông ABC, ta có
AC2 = BC2 – AB2 = 112 – 62 = 85, suy ra \(AC = \sqrt {85} \approx 9,2\) cm.
\(\sin B = \frac{{AC}}{{BC}} = \frac{{9,2}}{{11}} \approx 0,83,\) suy ra \(\widehat B \approx 57^\circ .\)
Từ đó suy ra \(\widehat C = 90^\circ - \widehat B = 90^\circ - 57^\circ = 33^\circ .\)
b) Trong tam giác vuông ABH, ta có
\(\sin B = \frac{{AH}}{{AB}},\) suy ra \(AH = AB.\sin B = 6.\sin 57^\circ \approx 5\) cm.
Vì AD là đường phân giác nên \(\widehat {BAD} = \frac{{\widehat {BAC}}}{2} = \frac{{90^\circ }}{2} = 45^\circ .\)
Trong tam giác vuông ABH, ta có \(\widehat {BAH} = 90^\circ - \widehat B = 90^\circ - 57^\circ = 33^\circ .\)
Do đó \(\widehat {HAD} = \widehat {BAD} - \widehat {BAH} = 45^\circ - 33^\circ = 12^\circ .\)
Trong tam giác ADH vuông tại H, ta có \(\cos \widehat {HAD} = \frac{{AH}}{{AD}},\)
suy ra \(AD = \frac{{AH}}{{\cos \widehat {HAD}}} = \frac{5}{{\cos 12^\circ }} \approx 5,1\) cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo