Cho tam giác ABC vuông tại A, biết AB = 6 cm, BC = 11 cm.
a) Giải tam giác vuông ABC.
b) Tính độ dài đường cao AH, đường phân giác AD.
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).
Cho tam giác ABC vuông tại A, biết AB = 6 cm, BC = 11 cm.
a) Giải tam giác vuông ABC.
b) Tính độ dài đường cao AH, đường phân giác AD.
(Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Bài tập cuối chương 4 có đáp án !!
Quảng cáo
Trả lời:
(H.4.45)
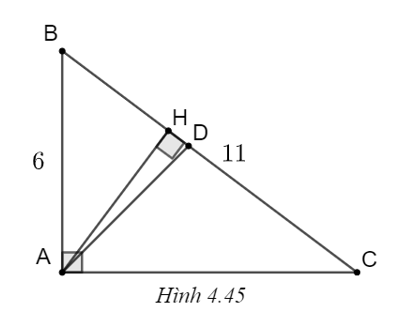
a) Trong tam giác vuông ABC, ta có
AC2 = BC2 – AB2 = 112 – 62 = 85, suy ra \(AC = \sqrt {85} \approx 9,2\) cm.
\(\sin B = \frac{{AC}}{{BC}} = \frac{{9,2}}{{11}} \approx 0,83,\) suy ra \(\widehat B \approx 57^\circ .\)
Từ đó suy ra \(\widehat C = 90^\circ - \widehat B = 90^\circ - 57^\circ = 33^\circ .\)
b) Trong tam giác vuông ABH, ta có
\(\sin B = \frac{{AH}}{{AB}},\) suy ra \(AH = AB.\sin B = 6.\sin 57^\circ \approx 5\) cm.
Vì AD là đường phân giác nên \(\widehat {BAD} = \frac{{\widehat {BAC}}}{2} = \frac{{90^\circ }}{2} = 45^\circ .\)
Trong tam giác vuông ABH, ta có \(\widehat {BAH} = 90^\circ - \widehat B = 90^\circ - 57^\circ = 33^\circ .\)
Do đó \(\widehat {HAD} = \widehat {BAD} - \widehat {BAH} = 45^\circ - 33^\circ = 12^\circ .\)
Trong tam giác ADH vuông tại H, ta có \(\cos \widehat {HAD} = \frac{{AH}}{{AD}},\)
suy ra \(AD = \frac{{AH}}{{\cos \widehat {HAD}}} = \frac{5}{{\cos 12^\circ }} \approx 5,1\) cm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
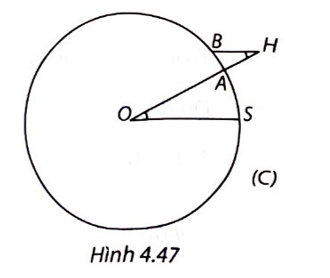
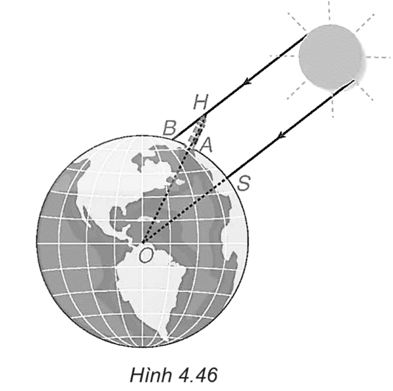
Trên Hình 4.47 đường tròn (C) với tâm O là tâm Trái Đất, đi qua S (Syene), A (Alexandria), OS = OA = R (R là bán kính của đường tròn (C)).
Theo giả thiết, cung tròn (nhỏ) SA của (C) dài 800 km.
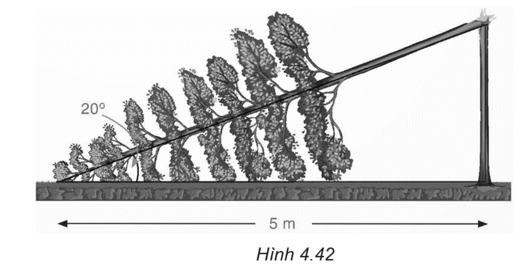
Gọi H là đỉnh tháp, chân tại A thì A nằm giữa O và H, AH = 25 m. Bóng của tháp là cung tròn AB của (C).
Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}.\)
Vì AH = 25 m khá bé so với R, Erastosthene coi cung tròn AB của (C) là một đoạn thẳng AB = 3,1 m vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có
\(\tan \widehat {AHB} = \frac{{AB}}{{AH}} = \frac{{3,1}}{{25}} = 0,124.\)
Suy ra \(\tan \widehat {{\rm{AOS}}} = 0,124\) nên \(\widehat {AOS} \approx 7^\circ .\)
Vì độ dài cung tròn MN tùy ý trên đường tròn tâm O tỉ lệ thuận với số đo góc ở tâm \(\widehat {MON},\) mà độ dài cung AS bằng 800 km ứng với góc ở tâm \(\widehat {AOS} \approx 7^\circ \) nên toàn bộ đường tròn (C) ứng với góc ở tâm 360° có độ dài xấp xỉ bằng
\(\frac{{360^\circ }}{{7^\circ }}.800 \approx 41142\) (km).
Vậy chu vi của Trái Đất xấp xỉ 41142 km.
Lời giải
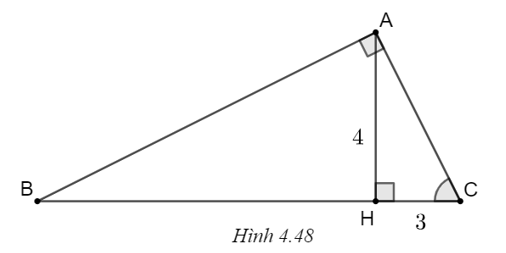
a) Trong tam giác AHC vuông tại H, theo định lí Pythagorem ta có
AC2 = AH2 + HC2 = 42 + 32 = 25 nên \(AC = \sqrt {25} = 5.\)
\(\tan C = \frac{{AH}}{{CH}} = \frac{4}{3},\) suy ra \(\widehat C \approx 53^\circ .\)
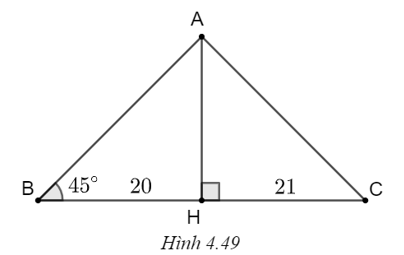
Tam giác ABC vuông ở A nên ta có
\(\widehat B = 90^\circ - \widehat C = 90^\circ - 53^\circ = 37^\circ ,\)
\(\tan C = \frac{{AB}}{{AC}}\) nên \(AB = AC.\tan C = 5.\tan 53^\circ = \frac{{20}}{3} \approx 6,7.\)
Theo định lí Pythagore, ta có
\(B{C^2} = A{B^2} + A{C^2} = {6,7^2} + {5^2} = 69,89\) nên \(BC = \sqrt {69,89} = 8,4\)
b) Tam giác ABH vuông tại H, theo định lí Pythagore, ta có
\(B{H^2} = A{B^2} - A{H^2} = {6,7^2} - {4^2} = 28,89\) nên \(BH = \sqrt {28,89} = 5,4.\)
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}} = \frac{{5,4}}{{6,7}}\) nên \(\widehat {BAH} \approx 54^\circ .\)
c) Ta có
\(M = \frac{{\sin B + 3\cos B}}{{\cos B}} = \frac{{\sin B}}{{\cos B}} + 3\)
\( = \tan B + 3 = \frac{3}{4} + 3 = \frac{{15}}{4} = 3,75.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.