Câu hỏi:
17/09/2024 1,492
Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).
a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?
b) Giả sử bán kính của (T1) và (T2) lần lượt là R1 và R2. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng \(\frac{1}{2}{R_1}\) và có bán kính bằng \(\frac{1}{2}{R_2}.\) Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mỗi đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu R1 = 3 cm và R2 = 2 cm.
Khi chuyển động, giả sử đầu mũi kim dài của một chiếc đồng hồ vạch nên một đường tròn, kí hiệu là (T1), trong khi đầu mũi kim ngắn vạch nên một đường tròn khác, kí hiệu là (T2).
a) Hai đường tròn (T1) và (T2) có vị trí tương đối như thế nào?
b) Giả sử bán kính của (T1) và (T2) lần lượt là R1 và R2. Người ta vẽ trên mặt đồng hồ một họa tiết hình tròn có tâm nằm cách điểm trục kim đồng hồ một khoảng bằng \(\frac{1}{2}{R_1}\) và có bán kính bằng \(\frac{1}{2}{R_2}.\) Hãy cho biết vị trí tương đối của đường tròn (T3) đối với mỗi đường tròn (T1) và (T2). Vẽ ba đường tròn đó nếu R1 = 3 cm và R2 = 2 cm.
Câu hỏi trong đề: Giải VTH Toán 9 KNTT Luyện tập chung có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
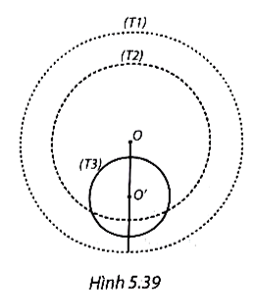
a) (T1) và (T2) là hai đường tròn đồng tâm với tâm O là điểm trục của hai kim đồng hồ.
b) (T2) là đường tròn tạo bởi đầu kim ngắn nên R2 < R1. (1)
Gọi O' là tâm và R3 là bán kính của đường tròn (T3). Theo đề bài, ta có:
\({R_3} = \frac{1}{2}{R_2}\) và \(OO' = \frac{1}{2}{R_1}.\) (2)
• Xét hai đường tròn (T1) và (T3), tức là hai đường tròn có bán kính R1 và R3.
Từ (1) và (2), ta có:
\({R_1} - {R_3} = {R_1} - \frac{1}{2}{R_2} = \frac{1}{2}\left( {{R_1} - {R_2}} \right) + \frac{1}{2}{R_1} > \frac{1}{2}{R_1},\) suy ra R1 – R3 > OO'.
Do đó (T1) đựng (T3).
• Xét hai đường tròn (T2) và (T3), tức là hai đường tròn có bán kính R2 và R3.
Từ (2) ta có:
\({R_2} - {R_3} = {R_2} - \frac{1}{2}{R_2} = \frac{1}{2}{R_2} > 0.\) (3)
Mặt khác, \({R_2} + {R_3} = {R_2} + \frac{1}{2}{R_2} = \frac{3}{2}{R_2}.\) Do đó:
− Nếu 3R2 > R1 thì \({R_2} + {R_3} = \frac{3}{2}{R_2} > \frac{1}{2}{R_1} = OO',\) tức là \({R_2} + {R_3} > OO'.\)
Kết hợp với (3) ta thấy (T2) và (T3) cắt nhau.
− Nếu 3R2 = R1 thì \({R_2} + {R_3} = \frac{3}{2}{R_2} = \frac{1}{2}{R_1} = OO',\) tức là \({R_2} + {R_3} = OO'\) và ta có (T2), (T3) tiếp xúc nhau.
− Nếu 3R2 < R1 thì \({R_2} + {R_3} = \frac{3}{2}{R_2} < \frac{1}{2}{R_1} = OO',\) tức là \({R_2} + {R_3} < OO'\) và ta có (T2) và (T3) không giao nhau.
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
(H.5.41)
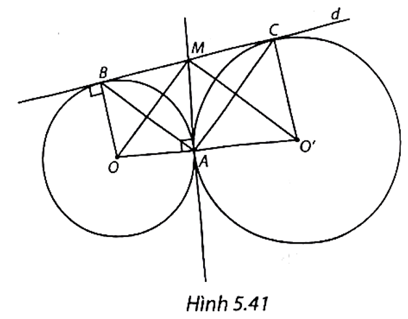
a) Hai đường tròn (O) và (O') tiếp xúc ngoài với nhau nên A ∈ (O').
Vì MA là tiếp tuyến của (O) tại A nên A ∈ (O), từ đó suy ra MA tiếp xúc với (O') tại A. Do đó MA là tiếp tuyến của (O') tại A.
b) MA và MB là hai tiếp tuyến của (O) tại M nên MA = MB.
Tương tự đối với đường tròn (O'), ta cũng có MA = MC.
Do đó MB = MC = MA.
Vậy M là trung điểm của BC.
Tam giác ABC có đường trung tuyến MA bằng một nửa cạnh huyền BC nên tam giác ABC là tam giác vuông.
Lời giải
(H.5.40)
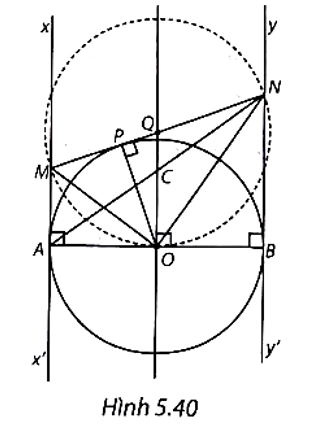
a) Ta có MN = MP + NP. Mặt khác, MA và MP là hai tiếp tuyến cắt nhau của (O) nên MA = MP. Tương tự, ta cũng có NB = NP.
Cộng từng vế hai đẳng thức trên ta được:
MA + NB = MP + NP (điều phải chứng minh).
b) Do OQ ⊥ AB (giả thiết), MA ⊥ AB và MB ⊥ AB (MA, MB là tiếp tuyến của (O) tại A và B) nên OQ // MA // MB. Nối A với N cắt OQ tại C.
Trong tam giác ABN, đường thẳng OQ đi qua trung điểm của cạnh AB và song song với BN nên C là trung điểm của trung điểm của AN.
Trong tam giác AMN, đường thẳng OQ đi qua trung điểm của AN và song song với AM nên Q là trung điểm của MN.
c) Theo tính chất của hai tiếp tuyến cắt nhau, OM là tia phân giác của góc \(\widehat {AOP}\) và ON là tia phân giác của góc \(\widehat {BOP}.\) Khi đó:
\(\widehat {MON} = \widehat {MOP} + \widehat {NOP} = \frac{1}{2}\widehat {AOP} + \frac{1}{2}\widehat {BOP}\)
\( = \frac{1}{2}\left( {\widehat {AOP} + \widehat {BOP}} \right) = \frac{1}{2}.180^\circ = 90^\circ .\)
Do đó tam giác MON là tam giác vuông tại O với OQ là đường trung tuyến.
Từ đó ta có OQ = MQ = NQ.
Do đó, đường tròn đường kính MN, cũng là đường tròn tâm Q đi qua O. Do đó AB cắt nhau và vuông góc với QO tại O.
Suy ra AB là tiếp tuyến của đường tròn đường kính MN.
Nói cách khác, AB tiếp xúc với đường tròn đường kính MN.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Dạng 5: Bài toán về lãi suất ngân hàng có đáp án
-
123 bài tập Nón trụ cầu và hình khối có lời giải
-
Đề thi minh họa TS vào 10 năm học 2025 - 2026_Môn Toán_Tỉnh Đắk Lắk
-
Dạng 2: Kỹ thuật chọn điểm rơi trong bài toán cực trị xảy ra ở biên có đáp án
-
Dạng 6: Bài toán về tăng giá, giảm giá và tăng, giảm dân số có đáp án
-
15 câu Trắc nghiệm Toán 9 Kết nối tri thức Bài 1. Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn có đáp án
-
Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án - Đề 01
-
Tổng hợp các bài toán thực tế ôn thi vào 10 Toán 9 có đáp án (Phần 2: Hình học)
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận