Cho hình hộp chữ nhật ABCD.A'B'C'D' có DA = 2, DC = 3, DD' = 2. Tính khoảng cách từ đỉnh B' đến mặt phẳng (BA'C').
Cho hình hộp chữ nhật ABCD.A'B'C'D' có DA = 2, DC = 3, DD' = 2. Tính khoảng cách từ đỉnh B' đến mặt phẳng (BA'C').
Quảng cáo
Trả lời:
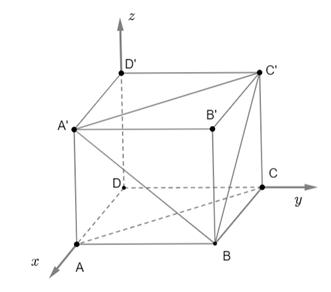
Chọn hệ tọa độ Oxyz sao cho gốc tọa độ O trùng với điểm D.
Khi đó, tọa độ các đỉnh của hình chữ nhật ABCD.A'B'C'D' lần lượt là D(0; 0; 0),
A(2; 0; 0), C(0; 3; 0), B(2; 3; 0), D'(0; 0; 2), A'(2; 0; 2), B'(2; 3; 2), C'(0; 3; 2).
Mặt phẳng (BA'C') có cặp vectơ chỉ phương là \[\overrightarrow {BA'} = \left( {0; - 3;2} \right)\], \[\overrightarrow {BC'} = \left( { - 2;0;2} \right)\].
Ta có: \[\overrightarrow n = \left[ {\overrightarrow {BA'} ,\overrightarrow {BC'} } \right] = \left( {\left| {\begin{array}{*{20}{c}}{ - 3}&2\\0&2\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&0\\2&{ - 2}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&{ - 3}\\{ - 2}&0\end{array}} \right|} \right)\] = (−6; −4; −6) = −2(3; 2; 3).
Do đó, \[\overrightarrow n \] = (3; 2; 3). Phương trình mặt phẳng (BA'C') là:
3(x – 2) + 2(y – 3) + 3z = 0 hay 3x + 2y + 3z – 12 = 0.
Khoảng cách từ đỉnh B' đến mặt phẳng (BA'C') là:
d(B', (BA'C')) = \[\frac{{\left| {3.2 + 2.3 + 3.2 - 12} \right|}}{{\sqrt {{3^2} + {2^2} + {3^2}} }} = \frac{{3\sqrt {22} }}{{11}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
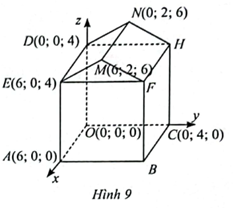
a) Ta có: \[\overrightarrow {DE} = \left( {6;0;0} \right),\overrightarrow {DN} = \left( {0;2;2} \right)\].
Ta có: \[\overrightarrow n = \left[ {\overrightarrow {DE} ,\overrightarrow {DN} } \right] = \left( {\left| {\begin{array}{*{20}{c}}0&0\\2&2\end{array}} \right|;\left| {\begin{array}{*{20}{c}}0&6\\2&0\end{array}} \right|;\left| {\begin{array}{*{20}{c}}6&0\\0&2\end{array}} \right|} \right)\] = (0; −12; 12) = −12(0; 1; −1).
Vậy \[\overrightarrow n = \left( {0;1; - 1} \right)\] là vectơ pháp tuyến của mặt phẳng (DEMN).
Phương trình của mặt phẳng (DEMN) là 1(y – 0) – 1(z – 4) = 0 hay y – z + 4 = 0.
b) Ta có B(6; 4; 0) nên d(B,(DEMN)) = \[\frac{{\left| {4 + 4} \right|}}{{\sqrt {{0^2} + {1^2} + {{\left( { - 1} \right)}^2}} }} = \frac{8}{{\sqrt 2 }} = 4\sqrt 2 \].
Lời giải
a) Xét hai mặt phẳng (P): 2x + y + 2z + 12 = 0, (Q): 4x + 2y + 4z – 6 = 0, ta có:
\[\frac{2}{4} = \frac{1}{2} = \frac{2}{4} \ne \frac{{12}}{{ - 6}}\] nên (P) ∥ (Q).
b) Trên mặt phẳng (Q) lấy M(0; 1; 1) ∈ (Q).
Ta có: P((P), (Q)) = d(M, (P)) = \[\frac{{\left| {2.0 + 1.1 + 2.1 + 12} \right|}}{{\sqrt {{2^2} + {1^2} + {2^2}} }} = \frac{{15}}{3}\]= 5.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.