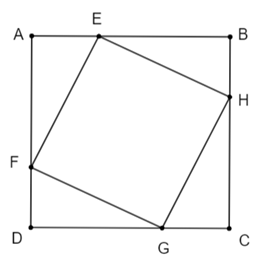
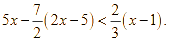Bác An có mảnh vườn hình vuông \[ABCD\] có cạnh bằng \[4{\rm{ m}}\]. Ở bốn góc vườn, bác An muốn trồng hoa vào các phần đất hình tam giác vuông bằng nhau (hình vẽ). Hãy tính khoảng cách từ góc vườn \[A\] đến vị trí \[E\] sao cho tứ giác \[EFGH\] có chu vi nhỏ nhất.

Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 9 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Đặt \[AE = x\,\,\left( {\rm{m}} \right){\rm{ }}\left( {0 < x < 4} \right)\]. Khi đó, \[EB = 4 - x{\rm{ }}\left( {\rm{m}} \right).\]
Theo đề, các phần đất hình tam giác bằng nhau, nên ta có:
\[AE = BH = GC = DF = x{\rm{ }}\left( {\rm{m}} \right)\] và \[BE = CH = GD = AF = 4 - x{\rm{ }}\left( {\rm{m}} \right)\].
Áp dụng định lí Pythagore vào tam giác \[AEF\] vuông tại \(A\), có:
\[A{E^2} + A{F^2} = E{F^2}\]
\[{x^2} + {\left( {4 - x} \right)^2} = E{F^2}\]
\[2{x^2} - 8x + 16 = E{F^2}\]
Suy ra \[EF = \sqrt {2{x^2} - 8x + 16} = \sqrt {2\left( {{x^2} - 4x + 4} \right) + 8} = \sqrt {2{{\left( {x - 2} \right)}^2} + 8} {\rm{ }}\left( {\rm{m}} \right).\]
Do các phần hình tam giác bằng nhau nên \[FG = GH = HE = EF = \sqrt {2{{\left( {x - 2} \right)}^2} + 8} {\rm{ }}\left( {\rm{m}} \right)\].
Suy ra, chu vi \[EFGH\] là: \[EF + FG + GH + HE = 4EF = 4\sqrt {2{{\left( {x - 2} \right)}^2} + 8} {\rm{ }}\left( {\rm{m}} \right)\].
Để chu vi của tứ giác \[EFGH\] nhỏ nhất thì \[4\sqrt {2{{\left( {x - 2} \right)}^2} + 8} \] nhỏ nhất.
Với mọi \[0 < x < 4,\] ta có:
\[2{\left( {x - 2} \right)^2} \ge 0\]
\[2{\left( {x - 2} \right)^2} + 8 \ge 8\]
\[\sqrt {2{{\left( {x - 2} \right)}^2} + 8} \ge \sqrt 8 \]
\[4\sqrt {2{{\left( {x - 2} \right)}^2} + 8} \ge 4\sqrt 8 \]
\[4\sqrt {2{{\left( {x - 2} \right)}^2} + 8} \ge 8\sqrt 2 \].
Do đó, chu vi của tứ giác \[EFGH\] nhỏ nhất bằng \[8\sqrt 2 {\rm{ m}}\] khi \[x - 2 = 0\] hay \[x = 2{\rm{ }}\left( {\rm{m}} \right).\]
Vậy khoảng cách từ \[A\] đến \[E\] bằng \[2{\rm{ m}}\] thì tứ giác \[EFGH\] có chu vi nhỏ nhất.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi ![]() (giờ) lần lượt là số giờ tổ I, tổ II làm riêng để hoàn thành toàn bộ công việc
(giờ) lần lượt là số giờ tổ I, tổ II làm riêng để hoàn thành toàn bộ công việc ![]()
⦁ Trong 1 giờ, tổ I làm được ![]() (công việc); tổ II làm được
(công việc); tổ II làm được ![]() (công việc).
(công việc).
Khi đó, trong 1 giờ, cả hai tổ làm được: ![]() (công việc).
(công việc).
Theo bài, nếu cả hai tổ cùng làm thì sau ![]() giờ xong công việc nên trong 1 giờ cả hai tổ làm chung được
giờ xong công việc nên trong 1 giờ cả hai tổ làm chung được ![]() (công việc). Ta có phương trình
(công việc). Ta có phương trình ![]() (1)
(1)
⦁ Trong 3 giờ, tổ I làm được ![]() (công việc).
(công việc).
Trong 5 giờ, tổ II làm được ![]() (công việc).
(công việc).
Theo bài, tổ I làm trong 3 giờ, tổ II làm trong 5 giờ thì hoàn thành được ![]() công việc nên ta có phương trình:
công việc nên ta có phương trình: ![]() (2).
(2).
Từ (1) và (2), ta có hệ phương trình: 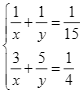 .
.
Từ phương trình thứ nhất, ta được: ![]() .
.
Thế ![]() vào phương trình thứ hai, ta được:
vào phương trình thứ hai, ta được:
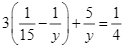 hay
hay ![]() , suy ra
, suy ra ![]() nên
nên ![]() (thỏa mãn).
(thỏa mãn).
Thay ![]() vào phương trình
vào phương trình ![]() , ta được:
, ta được:
![]() hay
hay ![]() , suy ra
, suy ra ![]() (thỏa mãn).
(thỏa mãn).
Vậy tổ I làm riêng trong 24 giờ sẽ hoàn thành công việc, tổ II làm riêng trong 40 giờ sẽ hoàn thành công việc.
Lời giải

⦁ Xét đường tròn ![]() có
có ![]() là hai tiếp cắt nhau tại
là hai tiếp cắt nhau tại ![]() nên
nên ![]() (tính chất hai tiếp tuyến cắt nhau). Do đó
(tính chất hai tiếp tuyến cắt nhau). Do đó ![]() thuộc đường trung trực
thuộc đường trung trực ![]() .
.
Mặt khác, ![]() nên
nên ![]() thuộc trung trực của đoạn thẳng
thuộc trung trực của đoạn thẳng ![]() .
.
Suy ra ![]() là đường trung trực của đoạn thẳng
là đường trung trực của đoạn thẳng ![]() , do đó
, do đó ![]() tại
tại ![]() .
.
⦁ Vì ![]() là tiếp tuyến của đường tròn
là tiếp tuyến của đường tròn ![]() tại
tại ![]() nên
nên ![]() tại
tại ![]()
Xét ![]() và
và ![]() có:
có: ![]() và
và ![]() là góc chung.
là góc chung.
Do đó ![]() (g.g)
(g.g)
Suy ra ![]() hay
hay ![]() (1).
(1).
Xét ![]() vuông tại
vuông tại ![]() ta có:
ta có: ![]() (định lí Pythagore). (2)
(định lí Pythagore). (2)
Lại có:
![]()
![]()
![]()
![]() (vì
(vì ![]() (3)
(3)
Từ (1), (2), (3) suy ra ![]()
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.