Hằng ngày mực nước của một con kênh lên xuống theo thủy triều. Độ sâu h (m) của mực nước trong kênh tại thời điểm t (giờ) (0 ≤ t ≤ 24) trong ngày được xác định bởi công thức \(h = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\). Tìm khoảng thời gian trong ngày mà độ sâu của mực nước trong kênh tăng dần.
A. (0; 8);
B. (8; 20);
C. (20; 24);
D. (8; 24).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
Ta có \(h\left( t \right) = 2\cos \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) + 5\)\( \Rightarrow h'\left( t \right) = - \frac{\pi }{6}\sin \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right)\).
\(h'\left( t \right) = 0 \Leftrightarrow \sin \left( {\frac{{\pi t}}{{12}} + \frac{\pi }{3}} \right) = 0 \Leftrightarrow \frac{{\pi t}}{{12}} + \frac{\pi }{3} = k\pi \)\( \Leftrightarrow t = - 4 + 12k\,\,\left( {k \in \mathbb{Z}} \right)\).
Mà 0 ≤ t ≤ 24 nên \(0 \le - 4 + 12k \le 24 \Leftrightarrow \frac{1}{3} \le k \le \frac{7}{3}\) k ∈ {1; 2}.
Do đó h'(t) = 0 t = 8 hoặc t = 20.
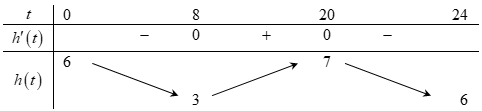
h(t) đồng biến trên khoảng (8; 20) hay trong khoảng từ 8 giờ đến 20 giờ độ sâu của mực nước trong kênh tăng dần.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\frac{{90}}{{19}}\);
B. \(\frac{{15\sqrt 2 }}{2}\);
C. \(\frac{{15}}{2}\);
D. \(\sqrt 2 \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: B
Xét hàm số \[y = C(x) = \frac{{30x}}{{{x^2} + 2}}\] trên khoảng x ∈ (0; 6).
Ta có: \[y' = \frac{{ - 30{x^2} + 60}}{{{{\left( {{x^2} + 2} \right)}^2}}}\].
\[y' = 0 \Leftrightarrow \frac{{ - 30{x^2} + 60}}{{{{\left( {{x^2} + 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \sqrt 2 \\x = - \sqrt 2 \,\end{array} \right.\]do x ∈ (0; 6)\[ \Rightarrow x = \sqrt 2 \].
Bảng biến thiên:
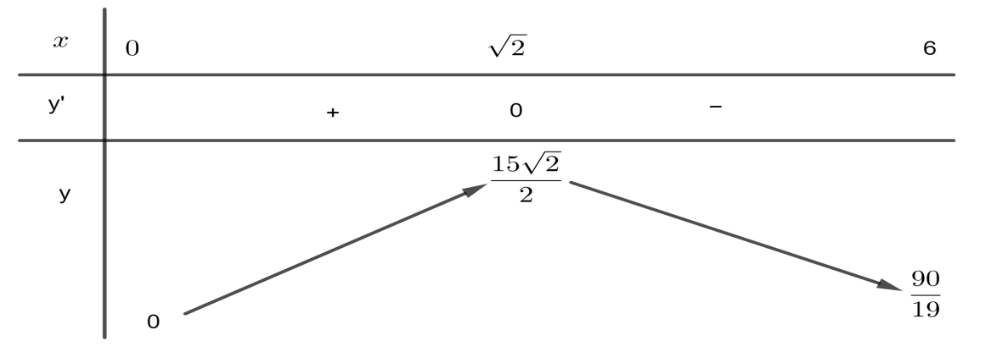
Từ bảng biến thiên suy ra: nồng độ thuốc trong máu C(x) đạt giá trị cực đại là \[\frac{{15\sqrt 2 }}{2}\left( {{\rm{mg/l}}} \right)\] trong khoảng thời gian 6 phút sau khi tiêm.
Câu 2
A. Vận tốc tăng trong khoảng thời gian t ∈ (3; 10) và giảm trong khoảng thời gian t ∈ (1; 3);
B. Vận tốc giảm trong khoảng thời gian t ∈ (2; 10) và tăng trong khoảng thời gian t ∈ (0; 2);
C. Vận tốc tăng trong khoảng thời gian t ∈ (1; 2) và giảm trong khoảng thời gian t ∈ (0; 1);
D. Vận tốc tăng trong khoảng thời gian t ∈ (2; 10) và giảm trong khoảng thời gian t ∈ (0; 2).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: D
Ta có v(t) = x'(t) = 3t2 – 12t + 9.
Xét v(t) = 3t2 – 12t + 9
v'(t) = 6t – 12 = 0 t = 2.
Bảng biến thiên
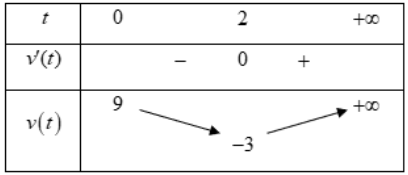
Vận tốc tăng trong khoảng thời gian t ∈ (2; 10) và giảm trong khoảng thời gian t ∈ (0; 2).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Tăng;
B. Giảm;
C. Tăng rồi giảm;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. (0; 15);
B. (0; 10);
C. (15; 25);
D. (10; 25).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. (0; 20);
B. (4; 20);
C. (12; +∞);
D. (0; 12).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập