Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc với nhau. Biết rằng \(AB = AC = a,AD = a\sqrt 3 \).
a) \[AC \bot \left( {ABD} \right)\].
d) \(\left( {CD,\left( {ABD} \right)} \right) = 30^\circ \).
c) Góc nhị diện \[\left[ {A,BC,D} \right]\] có số đo bằng \[87,79^\circ \].
d) Số đo của góc nhị diện \(\left[ {C,AB,D} \right]\) bằng \(90^\circ \).
Cho tứ diện \(ABCD\) có \(AB,AC,AD\) đôi một vuông góc với nhau. Biết rằng \(AB = AC = a,AD = a\sqrt 3 \).
a) \[AC \bot \left( {ABD} \right)\].
d) \(\left( {CD,\left( {ABD} \right)} \right) = 30^\circ \).
c) Góc nhị diện \[\left[ {A,BC,D} \right]\] có số đo bằng \[87,79^\circ \].
d) Số đo của góc nhị diện \(\left[ {C,AB,D} \right]\) bằng \(90^\circ \).
Câu hỏi trong đề: 50 bài tập Hình học không gian có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
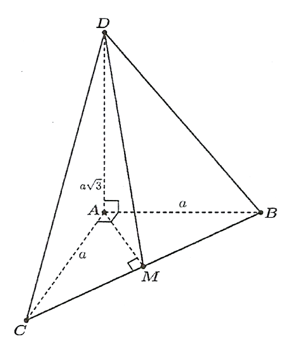
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AC \bot AB}\\{AC \bot AD}\end{array} \Rightarrow AC \bot \left( {ABD} \right)} \right.\).
Khi đó \(AD\) là hình chiếu của \(CD\) trên \(\left( {ABD} \right)\).
Ta có: \(\left( {CD,\left( {ABD} \right)} \right) = \left( {CD,AD} \right) = \widehat {CDA}\).
Tam giác \(ACD\) vuông tại \(A\) có:
\(\tan \widehat {CDA} = \frac{{AC}}{{AD}} = \frac{a}{{a\sqrt 3 }} = \frac{1}{{\sqrt 3 }} \Rightarrow \widehat {CDA} = 30^\circ \).
Vậy \(\left( {CD,\left( {ABD} \right)} \right) = \widehat {CDA} = 30^\circ \).Gọi \(M\) là trung điểm \(BC\) thì \(AM \bot BC\) (do \(AB = AC\)).
Vì \(\left\{ {\begin{array}{*{20}{l}}{AD \bot AB}\\{AD \bot AC}\end{array}} \right. \Rightarrow AD \bot \left( {ABC} \right) \Rightarrow AD \bot BC.\)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AM}\\{BC \bot AD}\end{array}} \right.\)\( \Rightarrow BC \bot \left( {ADM} \right)\)\( \Rightarrow BC \bot DM{\rm{.}}\)
Khi đó: \(\left( {AM,DM} \right) = \widehat {AMD}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,D} \right]\).
Tam giác \(ABC\) vuông cân tại \(A\) nên đường cao \(AM = \frac{{a\sqrt 2 }}{2}\).
Tam giác \(ADM\) vuông tại \(A\) có: \(\tan \widehat {AMD} = \frac{{AD}}{{AM}} = \frac{{a\sqrt 3 }}{{\frac{{a\sqrt 2 }}{2}}} = \sqrt 6 \Rightarrow \widehat {AMD} \approx 67,79^\circ \).
Vì \(AB \bot AC,AB \bot AD\) nên \(\left( {AC,AD} \right) = \widehat {CAD}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {C,AB,D} \right]\) và \(\widehat {CAD} = 90^\circ \).
Đáp án: a) Đúng, b) Đúng, c) Sai, d) Đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
![Cho lăng trụ đều \(ABC.A'B'C'\). Biết rằng góc nhị diện \(\left[ {A,BC,A'} \right]\) có số đo bằng \(30^\circ \), tam giác (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid12-1736864060.png)
Đặt \(AB = x,\left( {x > 0} \right)\), gọi \(M\) là trung điểm \(BC\).
Ta có \[\left\{ \begin{array}{l}AM \bot BC\\A'M \bot BC\end{array} \right.\], suy ra \(\widehat {A'MA}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {A,BC,A'} \right]\)\[ \Rightarrow \widehat {A'MA} = 30^\circ \].Xét \(\Delta A'AM\), có \[A'M = \frac{{AM}}{{cos30^\circ }} = \frac{{x\sqrt 3 }}{2} \cdot \frac{2}{{\sqrt 3 }} = x\].
\({S_{A'BC}} = 8 \Leftrightarrow \frac{1}{2}A'M \cdot BC = 8 \Leftrightarrow {x^2} = 16 \Rightarrow x = 4\).
Suy ra \(A'A = AM \cdot \tan 30^\circ = \frac{{4 \cdot \sqrt 3 }}{2} \cdot \frac{1}{{\sqrt 3 }} = 2\); \({S_{ABC}} = \frac{{16 \cdot \sqrt 3 }}{4} = 4\sqrt 3 \).
Vậy \({V_{ABC.A'B'C'}} = A'A \cdot {S_{ABC}} = 2 \cdot 4\sqrt 3 = 8\sqrt 3 \). Chọn A.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Ta có: \(AD\,{\rm{//}}\,BC \Rightarrow AD\,{\rm{//}}\,\,\left( {SBC} \right) \Rightarrow d\left( {D,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right)\).
Trong mặt phẳng \(\left( {SAB} \right)\), kẻ \(AH \bot SB\) tại \(H\). (1)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{BC \bot AB}\\{BC \bot SA}\end{array} \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow AH \bot BC} \right.\). (2)
Từ (1) và (2) suy ra \(AH \bot \left( {SBC} \right)\) hay \(d\left( {A,\left( {SBC} \right)} \right) = AH\).
Tam giác \(SAB\) vuông tại \(A\) có đường cao \(AH\) nên:
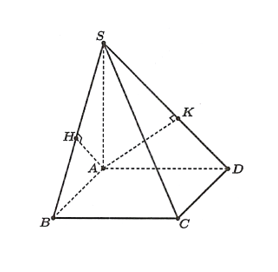
\(\frac{1}{{A{H^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{B^2}}} \Rightarrow AH = \frac{{SA \cdot AB}}{{\sqrt {S{A^2} + A{B^2}} }} = \frac{{2a \cdot a\sqrt 2 }}{{\sqrt {4{a^2} + 2{a^2}} }} = \frac{{2a\sqrt 3 }}{3}{\rm{. }}\)
Vậy \(d\left( {D,\left( {SBC} \right)} \right) = d\left( {A,\left( {SBC} \right)} \right) = AH = \frac{{2a\sqrt 3 }}{3}\).
Trong mặt phẳng \(\left( {SAD} \right)\), kẻ \(AK \bot SD\) tại \(K\). (3)
Ta có: \(\left\{ {\begin{array}{*{20}{l}}{AB \bot SA}\\{AB \bot AD}\end{array} \Rightarrow AB \bot \left( {SAD} \right) \Rightarrow AB \bot AK} \right.\).(4)
Từ (3) và (4) suy ra \(AK\) là đường vuông góc chung của hai đường thẳng chéo nhau \(AB,SD\).
Tam giác \(ACD\) vuông tại \(D\) nên \(AD = \sqrt {A{C^2} - C{D^2}} = \sqrt {3{a^2} - 2{a^2}} = a\).
Tam giác \(SAD\) vuông tại \(A\) có đường cao \(AK\) nên
\(\frac{1}{{A{K^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} \Rightarrow AK = \frac{{SA \cdot AD}}{{\sqrt {S{A^2} + A{D^2}} }} = \frac{{2a \cdot a}}{{\sqrt {4{a^2} + {a^2}} }} = \frac{{2a\sqrt 5 }}{5}{\rm{. }}\)
Vậy \(d\left( {AB,SD} \right) = AK = \frac{{2a\sqrt 5 }}{5}\).
Diện tích đáy hình chóp là: \({S_{ABCD}} = a \cdot a\sqrt 2 = {a^2}\sqrt 2 \).
Thể tích khối chóp cần tìm là: \({V_{S.ABCD}} = \frac{1}{3}SA \cdot {S_{ABCD}} = \frac{1}{3} \cdot 2a \cdot {a^2}\sqrt 2 = \frac{{2\sqrt 2 {a^3}}}{3}{\rm{ }}\)(đơn vị thể tích).
Đáp án: a) Đúng, b) Sai, c) Đúng, d) Sai.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
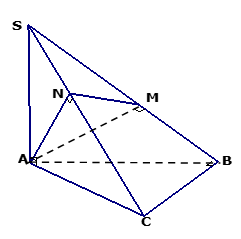
A. \[AM \bot SC\].
B. \[AM \bot MN\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập