Giá trị lớn nhất của hàm số \(f\left( x \right) = 2 + 2x - {e^x}\) trên đoạn \(\left[ {0;2} \right]\) bằng
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
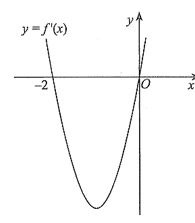
Ta có \(f'\left( x \right) = 2 - {e^x}\); \(f'\left( x \right) = 0 \Leftrightarrow {e^x} = 2 \Leftrightarrow x = \ln 2\).
Bảng biến thiên
![Giá trị lớn nhất của hàm số \(f\left( x \right) = 2 + 2x - {e^x}\) trên đoạn \(\left[ {0;2} \right]\) bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid1-1737208056.png)
Từ bảng biến thiên, ta có \(\mathop {\max }\limits_{\left[ {0;2} \right]} f\left( x \right) = f\left( {\ln 2} \right) = 2\ln 2\). Chọn D.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
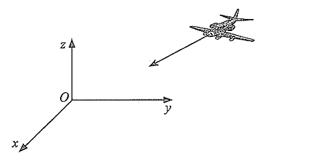
Giả sử \(A\left( { - 50;30;10} \right)\), \(B\left( {2;3;0} \right)\). Khi đó \(\overrightarrow {AB} = \left( {52; - 27; - 10} \right)\).
Gọi \(\alpha \)là góc tạo bởi đường bay của máy bay và mặt đất.
Khi đó ta có \(\sin \alpha = \sin \left( {AB,\left( {Oxy} \right)} \right) = \frac{{\left| {52 \cdot 0 + \left( { - 27} \right) \cdot 0 + \left( { - 10} \right) \cdot 1} \right|}}{{\sqrt {{{52}^2} + {{\left( { - 27} \right)}^2} + {{\left( { - 10} \right)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{10}}{{\sqrt {3533} }}\).
Suy ra \(\alpha \approx 9,69^\circ \).
Đáp án: \(9,69\).
Câu 2
Lời giải
Gọi biến cố V: “Viên bi lấy ra có màu vàng”, biến cố Đ: “Viên bi lấy ra có màu đỏ”,
biến cố X: “Viên bi lấy ra có màu xanh”.
Ta có \(P\left( X \right) = \frac{4}{8} = \frac{1}{2}\); . Khi đó, . Chọn D.
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.