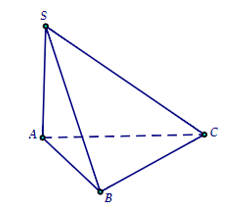
Cho hình chóp \(S.ABC\) có đáy là tam giác đều cạnh \(2\), \(SA\) vuông góc với đáy. Biết góc giữa mặt phẳng \(\left( {SBC} \right)\) và mặt đáy \(\left( {ABC} \right)\) bằng \(60^\circ \) (tham khảo hình vẽ bên). Tính thể tích khối chóp \(S.ABC\) (làm tròn kết quả đến hàng phần trăm).
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
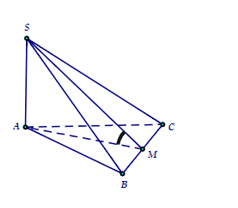
Ta có \({S_{ABC}} = \frac{{{2^2} \cdot \sqrt 3 }}{4} = \sqrt 3 \).
Gọi \(M\) là trung điểm \(BC\).
Suy ra \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \widehat {SMA}\).
Ta có \(\tan \widehat {SMA} = \frac{{SA}}{{AM}} \Rightarrow SA = AM \cdot \tan \widehat {SMA} = \sqrt 3 \cdot \sqrt 3 = 3\).
Vậy \({V_{S.ABC}} = \frac{1}{3}SA \cdot {S_{ABC}} = \frac{1}{3} \cdot 3 \cdot \sqrt 3 = \sqrt 3 \approx 1,73\).
Đáp án: \(1,73\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
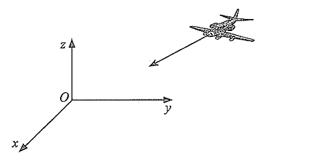
Giả sử \(A\left( { - 50;30;10} \right)\), \(B\left( {2;3;0} \right)\). Khi đó \(\overrightarrow {AB} = \left( {52; - 27; - 10} \right)\).
Gọi \(\alpha \)là góc tạo bởi đường bay của máy bay và mặt đất.
Khi đó ta có \(\sin \alpha = \sin \left( {AB,\left( {Oxy} \right)} \right) = \frac{{\left| {52 \cdot 0 + \left( { - 27} \right) \cdot 0 + \left( { - 10} \right) \cdot 1} \right|}}{{\sqrt {{{52}^2} + {{\left( { - 27} \right)}^2} + {{\left( { - 10} \right)}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{10}}{{\sqrt {3533} }}\).
Suy ra \(\alpha \approx 9,69^\circ \).
Đáp án: \(9,69\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi biến cố V: “Viên bi lấy ra có màu vàng”, biến cố Đ: “Viên bi lấy ra có màu đỏ”,
biến cố X: “Viên bi lấy ra có màu xanh”.
Ta có \(P\left( X \right) = \frac{4}{8} = \frac{1}{2}\); . Khi đó, . Chọn D.
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập