Khi kiểm tra sức khoẻ tổng quát của bệnh nhân ở một bệnh viện, người ta được kết quả như sau:
– Có \(40\% \) bệnh nhân bị đau dạ dày.
– Có \(30\% \) bệnh nhân thường xuyên bị stress.
– Trong số các bệnh nhân bị stress có \(80\% \) bệnh nhân bị đau dạ dày.
Chọn ngẫu nhiên 1 bệnh nhân.
a) Xác suất chọn được bệnh nhân thường xuyên bị stress là \(0,3\).
b) Xác suất chọn được bệnh nhân bị đau dạ dày, biết bệnh nhân đó thường xuyên bị stress, là \(0,8.\)
c) Xác suất chọn được bệnh nhân vừa thường xuyên bị stress vừa bị đau dạ dày là \(0,24.\)
d) Xác suất chọn được bệnh nhân thường xuyên bị stress, biết bệnh nhân đó bị đau dạ dày, là \(0,6.\)
Khi kiểm tra sức khoẻ tổng quát của bệnh nhân ở một bệnh viện, người ta được kết quả như sau:
– Có \(40\% \) bệnh nhân bị đau dạ dày.
– Có \(30\% \) bệnh nhân thường xuyên bị stress.
– Trong số các bệnh nhân bị stress có \(80\% \) bệnh nhân bị đau dạ dày.
Chọn ngẫu nhiên 1 bệnh nhân.
a) Xác suất chọn được bệnh nhân thường xuyên bị stress là \(0,3\).
b) Xác suất chọn được bệnh nhân bị đau dạ dày, biết bệnh nhân đó thường xuyên bị stress, là \(0,8.\)
c) Xác suất chọn được bệnh nhân vừa thường xuyên bị stress vừa bị đau dạ dày là \(0,24.\)
d) Xác suất chọn được bệnh nhân thường xuyên bị stress, biết bệnh nhân đó bị đau dạ dày, là \(0,6.\)
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Xét các biến cố: \(A\): “Chọn được bệnh nhân thường xuyên bị stress”;
\(B\): “Chọn được bệnh nhân bị đau dạ dày”.
Khi đó, \(P\left( A \right) = 0,3;P\left( B \right) = 0,4;P\left( {B\mid A} \right) = 0,8\).
Suy ra xác suất chọn được bệnh nhân thường xuyên bị stress vừa bị đau dạ dày là
\(P\left( {A \cap B} \right) = P\left( A \right) \cdot P\left( {B\mid A} \right) = 0,3 \cdot 0,8 = 0,24\);
Xác suất chọn được bệnh nhân thường xuyên bị stress, biết bệnh nhân đó bị đau dạ dày, là \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{{0,24}}{{0,4}} = 0,6\).
Đáp án: a) Đúng, b) Đúng, c) Đúng, d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(f\left( x \right)\) là lợi nhuận mà lái xe có thể thu về khi chở \(x\) (người) \(\left( {x \in {\mathbb{N}^*}} \right)\) trong chuyến xe đó.
Khi đó: \(f\left( x \right) = \frac{1}{2}x{\left( {40 - x} \right)^2}\), với \(0 < x \le 16\).
Ta có: \(f'\left( x \right) = \frac{1}{2}\left[ {{{\left( {40 - x} \right)}^2} - 2x\left( {40 - x} \right)} \right] = \frac{1}{2}\left( {40 - x} \right)\left( {40 - 3x} \right)\).
Với \(0 < x \le 16\) thì \(f'\left( x \right) = 0 \Leftrightarrow x = \frac{{40}}{3}\).
Mà \(13 < \frac{{40}}{3} < 14\) nên ta có bảng biến thiên như sau:
![Một xe ô tô chở khách du lịch có sức chứa tối đa là \[16\] hành khách. Trong một khu du lịch, một đoàn khách gồm (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid18-1737298185.png)
Với \(f\left( {13} \right) = 4738,5,\,\,f\left( {14} \right) = 4732\).
Căn cứ vào bảng biến thiên ta có \[\mathop {\max }\limits_{\left( {0;16} \right]} f\left( x \right) = 4738,5\] (nghìn đồng).
Vậy người lái xe đó có thể thu được nhiều nhất khoảng 4,74 triệu đồng từ một chuyến chở khách.
Đáp án: \(4,74\).
Lời giải
Ta có: \(\overrightarrow {AB} = \left( {2\,;\, - 2\,;\,0} \right)\), \(\overrightarrow {AC} = \left( {1\,;\, - 3\,;\, - 4} \right)\) và \(\left[ {\overrightarrow {AB} \,,\overrightarrow {AC} } \right] = \left( {8\,;\,8\,;\, - \,4} \right)\).
Suy ra mặt phẳng \(\left( P \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_1}} = \left( {2\,;\,\,2\,;\, - 1} \right)\).
Mặt phẳng \(\left( {Oxy} \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_2}} = \left( {0\,;\,\,0\,;\,1} \right)\).
Khi đó, \(\cos \left( {\left( P \right)\,,\,\left( {Oxy} \right)} \right) = \frac{{\left| {\overrightarrow {{n_1}} \, \cdot \,\,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|\,\, \cdot \,\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {2\, \cdot 0 + 2\, \cdot \,0 + \left( { - \,1} \right)\, \cdot 1} \right|}}{{\sqrt {{2^2} + {2^2} + {{\left( { - \,1} \right)}^2}} \, \cdot \sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{1}{3}.\)
Vậy góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {Oxy} \right)\) bằng khoảng \(71^\circ \).
Đáp án: \(71\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
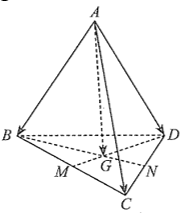
A. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 3\overrightarrow {AG} \).
B. \(\overrightarrow {AB} + \overrightarrow {AC} = 2\overrightarrow {AM} \).
C. \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AN} = 3\overrightarrow {AG} \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.