Câu hỏi:

19/01/2025 415

Số tiệm cận đứng của đồ thị hàm số $y = f\left( x \right) = \frac{{{x^2} + x - 2}}{{{x^2} - 4}}$ là

A. $0$.

B. $1$.

C. $2$.

D. $3$.

Xem lời giải

Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Tập xác định $D = \mathbb{R}\backslash \left\{ {2; - 2} \right\}$.

Ta có $y = f\left( x \right) = \frac{{{x^2} + x - 2}}{{{x^2} - 4}} = \frac{{\left( {x - 1} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{x - 1}}{{x - 2}}$.

$\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{x - 1}}{{x - 2}} = + \infty $; $\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{x - 1}}{{x - 2}} = - \infty $;

$\mathop {\lim }\limits_{x \to - {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ + }} \frac{{x - 1}}{{x - 2}} = \frac{3}{4}$; $\mathop {\lim }\limits_{x \to - {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to - {2^ - }} \frac{{x - 1}}{{x - 2}} = \frac{3}{4}$.

Suy ra đồ thị hàm số $y = f\left( x \right)$ có một tiệm cận đứng là đường thẳng $x = 2$. Chọn B.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Khi đặt hệ tọa độ \[Oxyz\]vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng một không gian phủ sóng điện thoại có dạng một hình cầu $\left( S \right)$ (tập hợp những điểm nằm trong và nằm trên mặt cầu tương ứng). Biết mặt cầu $\left( S \right)$ có phương trình: \[{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 5 = 0\]. Khoảng cách xa nhất giữa hai vùng phủ sóng là bao nhiêu kilômét?

$Khi đặt hệ tọa độ \[Oxyz\]vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng (ảnh 1)$

Xem đáp án

Lời giải

Ta có: ${x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 5 = 0 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = {3^2}$.

Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là đường kính của mặt cầu, tức là $6$km.

Đáp án: $6$.

Câu 2

Một chiếc bát thủy tinh có bề dày của phần xung quanh là một khối tròn xoay, khi xoay hình phẳng $D$ quanh một đường thẳng $a$ bất kì nào đó mà khi gắn hệ trục tọa độ $Oxy$ (đơn vị trên trục là decimét) vào hình phẳng $D$ tại một vị trí thích hợp, thì đường thẳng $a$ sẽ trùng với trục $Ox$. Khi đó hình phẳng $D$ được giới hạn bởi các đồ thị hàm số $y = x + \frac{1}{x}$, $y = x$ và hai đường thẳng $x = 1$, $x = 4$. Thể tích của bề dày chiếc bát thủy tinh đó bằng bao nhiêu decimét khối (làm tròn kết quả đến hàng phần mười)?

Xem đáp án

Lời giải

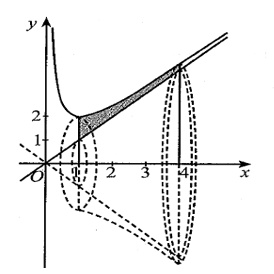
Gọi ${V_1}$ là thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = x + \frac{1}{x}$, trục hoành và hai đường thẳng $x = 1,x = 4$ quay quanh trục $Ox$.

Khi đó ${V_1} = \pi \int\limits_1^4 {{{\left( {x + \frac{1}{x}} \right)}^2}} \;{\rm{d}}x = \frac{{111\pi }}{4}\,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)$.

Gọi ${V_2}$ là thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số $y = x$, trục hoành và hai đường thẳng $x = 1,x = 4$ quay quanh trục $Ox$.

Khi đó ${V_2} = \pi \int\limits_1^4 {{x^2}} \;{\rm{d}}x = 21\,\pi \,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)$.

Vậy thể tích của bề dày chiếc bát thủy tinh đó là: $V = {V_1} - {V_2} = \frac{{111\pi }}{4} - 21\pi = \frac{{27\pi }}{4} \approx 21,2\,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right){\rm{.}}$

Đáp án: $21,2$.

Câu 3

Xác suất bắn trúng đích của xạ thủ hạng I là $0,8$ và của xạ thủ hạng II là $0,7$. Chọn ngẫu nhiên 1 xạ thủ từ một nhóm gồm 4 xạ thủ hạng I và 6 xạ thủ hạng II. Xạ thủ này bắn một viên đạn và viên đạn đó trúng mục tiêu, tính xác suất để đó là xạ thủ hạng I (làm tròn kết quả đến hàng phần trăm).

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Diện tích hình phẳng giới hạn bởi parabol $\left( P \right):y = f\left( x \right) = {x^2} - 1$, trục tung và tiếp tuyến của $\left( P \right)$ tại điểm $M\left( { - 1;0} \right)$ bằng

A. $\frac{5}{3}$.

B. $\frac{2}{3}$.

C. $\frac{1}{3}$.

D. $\frac{4}{3}$.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Bất phương trình ${\log _3}\left( {{x^2} - x + 7} \right) < 2$ có tập nghiệm là khoảng $\left( {a;b} \right)$. Tính $b - a$.

A. $b - a = - 1$.

B. $b - a = - 3$.

C. $b - a = 3$.

D. $b - a = 1$.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Trong không gian $Oxyz$, cho hai điểm $A\left( {1;2;3} \right)$, $B\left( {0;1; - 6} \right)$ và mặt phẳng $\left( P \right):4x - y + 2z + 13 = 0$.

a) Mặt phẳng $\left( P \right)$ đi qua điểm $A$.

b) Đường thẳng $\Delta $ đi qua điểm $A$ và vuông góc với mặt phẳng $\left( P \right)$ có phương trình tham số là $\left\{ \begin{array}{l}x = 1 + 4t\\y = 2 + t\\z = 3 + 2t\end{array} \right.$.

c) Điểm $C\left( { - 3;3;1} \right)$ là giao điểm của đường thẳng $\Delta $ và mặt phẳng $\left( P \right)$.

d) Gọi $d$ là một đường thẳng nằm trong $\left( P \right)$ và $d$ đi qua $B$ sao cho khoảng cách từ $A$ đến $d$ đạt giá trị nhỏ nhất. Một vectơ chỉ phương của $d$ có tọa độ là $\left( {a;b;c} \right)$ với $a$ là số nguyên tố. Giá trị của $a + b + c = 6$.

Xem đáp án

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Trong không gian tọa độ $Oxyz$, mặt cầu $\left( S \right)$ có tâm $I\left( {2;1; - 1} \right)$ và đường kính 6 có phương trình là

A. ${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 36$.

B. ${\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 9$.

C. ${\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 9$.

D. ${\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 36$.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay