Huấn luyện viên thống kê thời gian chạy cự li 200 m của hai vận động viên Hoa và Mai trong một đợt huấn luyện ở bảng sau.
Thời gian (giây)
\(\left[ {23,7;\,23,8} \right)\)
\(\left[ {23,8;\,23,9} \right)\)
\(\left[ {23,9;\,24} \right)\)
\(\left[ {24;\,24,1} \right)\)
\(\left[ {24,1;\,24,2} \right)\)
Số lần chạy của Hoa
11
15
7
0
5
Số lần chạy của Mai
28
18
4
0
0
a) Khoảng biến thiên thời gian chạy của hai vận động viên là như nhau.
b) Thành tích trung bình của Hoa đạt dưới 23,9 giây.
c) Nếu so sánh theo số trung bình thì thành tích của Hoa tốt hơn của Mai.
d) Nếu so sánh theo độ lệch chuẩn thì Mai có thành tích ổn định hơn Hoa.
Huấn luyện viên thống kê thời gian chạy cự li 200 m của hai vận động viên Hoa và Mai trong một đợt huấn luyện ở bảng sau.
|
Thời gian (giây) |
\(\left[ {23,7;\,23,8} \right)\) |
\(\left[ {23,8;\,23,9} \right)\) |
\(\left[ {23,9;\,24} \right)\) |
\(\left[ {24;\,24,1} \right)\) |
\(\left[ {24,1;\,24,2} \right)\) |
|
Số lần chạy của Hoa |
11 |
15 |
7 |
0 |
5 |
|
Số lần chạy của Mai |
28 |
18 |
4 |
0 |
0 |
a) Khoảng biến thiên thời gian chạy của hai vận động viên là như nhau.
b) Thành tích trung bình của Hoa đạt dưới 23,9 giây.
c) Nếu so sánh theo số trung bình thì thành tích của Hoa tốt hơn của Mai.
d) Nếu so sánh theo độ lệch chuẩn thì Mai có thành tích ổn định hơn Hoa.
Câu hỏi trong đề: Đề thi ôn tốt nghiệp THPT Toán có lời giải !!
Quảng cáo
Trả lời:
Khoảng biến thiên thời gian chạy của Hoa là \(24,2 - 23,7 = 0,5\) (giây).
Khoảng biến thiên thời gian chạy của Mai là \(24 - 23,7 = 0,3\)(giây).
Ta có bảng sau
|
Thời gian (giây) |
\(\left[ {23,7;23,8} \right)\) |
\(\left[ {23,8;23,9} \right)\) |
\(\left[ {23,9;24} \right)\) |
\(\left[ {24;24,1} \right)\) |
\(\left[ {24,1;24,2} \right)\) |
|
Giá trị đại diện |
\(23,75\) |
\(23,85\) |
\(23,95\) |
\(24,05\) |
\(24,15\) |
|
Số lần chạy của Hoa |
11 |
15 |
7 |
0 |
5 |
|
Số lần chạy của Mai |
28 |
18 |
4 |
0 |
0 |
Thành tích trung bình của Hoa là
\(\overline {{x_1}} = \frac{{23,75 \cdot 11 + 23,85 \cdot 15 + 23,95 \cdot 7 + 24,05 \cdot 0 + 24,15 \cdot 5}}{{38}} \approx 23,8789 < 23,9\).
Thành tích trung bình của Mai là
\(\overline {{x_2}} = \frac{{23,75 \cdot 28 + 23,85 \cdot 18 + 23,95 \cdot 4 + 24,05 \cdot 0 + 24,15 \cdot 0}}{{50}} = 23,802\).
Vì \(\overline {{x_2}} < \overline {{x_1}} \) nên thành tích trung bình của Mai tốt hơn Hoa.
Độ lệch chuẩn của mẫu số liệu về thời gian chạy của Hoa là
\({s_1} = \sqrt {\frac{{23,{{75}^2} \cdot 11 + 23,{{85}^2} \cdot 15 + 23,{{95}^2} \cdot 7 + 24,{{05}^2} \cdot 0 + 24,{{15}^2} \cdot 5}}{{38}} - 23,{{8789}^2}} \approx 0,134\).
Độ lệch chuẩn của mẫu số liệu về thời gian chạy của Mai là
\({s_2} = \sqrt {\frac{{23,{{75}^2} \cdot 28 + 23,{{85}^2} \cdot 18 + 23,{{95}^2} \cdot 4 + 24,{{05}^2} \cdot 0 + 24,{{15}^2} \cdot 0}}{{50}} - 23,{{802}^2}} = 0,064\).
Do độ lệch chuẩn của Mai thấp hơn của Hoa nên Mai có thành tích ổn định hơn Hoa.
Đáp án: a) Sai, b) Đúng, c) Sai, d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có: \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 5 = 0 \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = {3^2}\).
Khoảng cách xa nhất giữa hai điểm thuộc vùng phủ sóng là đường kính của mặt cầu, tức là \(6\)km.
Đáp án: \(6\).
Lời giải
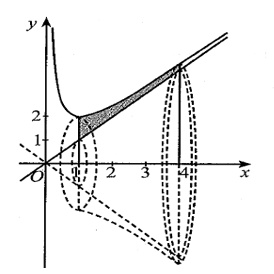
Gọi \({V_1}\) là thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(y = x + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1,x = 4\) quay quanh trục \(Ox\).
Khi đó \({V_1} = \pi \int\limits_1^4 {{{\left( {x + \frac{1}{x}} \right)}^2}} \;{\rm{d}}x = \frac{{111\pi }}{4}\,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\).
Gọi \({V_2}\) là thể tích của khối tròn xoay được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số \(y = x\), trục hoành và hai đường thẳng \(x = 1,x = 4\) quay quanh trục \(Ox\).
Khi đó \({V_2} = \pi \int\limits_1^4 {{x^2}} \;{\rm{d}}x = 21\,\pi \,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right)\).
Vậy thể tích của bề dày chiếc bát thủy tinh đó là: \(V = {V_1} - {V_2} = \frac{{111\pi }}{4} - 21\pi = \frac{{27\pi }}{4} \approx 21,2\,\,\left( {{\rm{d}}{{\rm{m}}^{\rm{3}}}} \right){\rm{.}}\)
Đáp án: \(21,2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 36\).
B. \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 9\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Khi đặt hệ tọa độ \[Oxyz\]vào không gian với đơn vị trên trục tính theo kilômét, người ta thấy rằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/01/blobid44-1737301480.png)