Người thứ nhất chèo thuyền với vận tốc 6 (km/h) vào bờ biển từ một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng \(AB = 4\left( {{\rm{km}}} \right)\). Trên bờ biển, người thứ hai đi xe máy với vận tốc 10 (km/h) từ một nhà kho ở vị trí C cách \(B\) một khoảng \(BC = 7\)(km) (hình vẽ bên dưới). Xác định vị trí hai người gặp nhau ở vị trí \(M\) đến \(C\), biết hai người xuất phát cùng một lúc (kết quả làm tròn đến hàng phần chục).
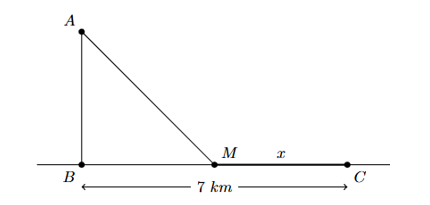
Người thứ nhất chèo thuyền với vận tốc 6 (km/h) vào bờ biển từ một ngọn hải đăng đặt tại vị trí \(A\) cách bờ biển một khoảng \(AB = 4\left( {{\rm{km}}} \right)\). Trên bờ biển, người thứ hai đi xe máy với vận tốc 10 (km/h) từ một nhà kho ở vị trí C cách \(B\) một khoảng \(BC = 7\)(km) (hình vẽ bên dưới). Xác định vị trí hai người gặp nhau ở vị trí \(M\) đến \(C\), biết hai người xuất phát cùng một lúc (kết quả làm tròn đến hàng phần chục).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Theo đề ta có \(BM = 7 - x\) (điều kiện \(0 < x < 7\))
Xét \(\Delta ABM\) ta có \(AM = \sqrt {A{B^2} + B{M^2}} = \sqrt {{4^2} + {{\left( {7 - x} \right)}^2}} \).
Theo đề ta có \(\frac{{\sqrt {{4^2} + {{\left( {7 - x} \right)}^2}} }}{6} = \frac{x}{{10}}\).
Bình phương hai vế phương trình ta được \(\frac{{65 - 14x + {x^2}}}{{36}} = \frac{{{x^2}}}{{100}}\)\( \Leftrightarrow 1625 - 350x + 25{x^2} = 9{x^2}\)
\( \Leftrightarrow 1625 - 350x + 16{x^2} = 0\)\( \Leftrightarrow x \approx 15,2\) hoặc \(x \approx 6,7\).
Thử lại ta thấy giá trị 6,7 thỏa mãn.
Vậy hai người gặp nhau ở vị trí M cách C một khoảng 6,7 km.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Theo đề ta có \(\left\{ \begin{array}{l}a - c = 147\\a + c = 152\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}a = \frac{{299}}{2}\\c = \frac{5}{2}\end{array} \right.\).
Tâm sai của elip \(\left( E \right)\) là \(e = \frac{c}{a} = \frac{5}{2}:\frac{{299}}{2} = \frac{5}{{299}}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Đ, b) S, c) Đ, d) S
Đường tròn \(\left( C \right)\) có tâm \(I\left( {3; - 1} \right);R = 2\).
a) Ta có \(IA = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( { - 1 + 1} \right)}^2}} = 2 = R\). Suy ra điểm \(A\) thuộc đường tròn.
b) Ta có \(IB = \sqrt {{{\left( {1 - 3} \right)}^2} + {{\left( {3 + 1} \right)}^2}} = 2\sqrt 5 > R\). Suy ra điểm \(B\) nằm ngoài đường tròn.
c) Có \(\overrightarrow {IA} = \left( { - 2;0} \right)\).
Phương trình tiếp tuyến của \(\left( C \right)\) tại điểm \(A\) đi qua \(A\left( {1; - 1} \right)\) và nhận \(\overrightarrow n = \left( { - 1;0} \right)\) làm vectơ pháp tuyến có phương trình là \( - \left( {x - 1} \right) = 0 \Leftrightarrow x = 1\).
d) Giả sử tiếp tuyến qua \(B\) nhận \(\overrightarrow n = \left( {a;b} \right)\) làm vectơ pháp tuyến có phương trình là
\(a\left( {x - 1} \right) + b\left( {y - 3} \right) = 0\)\( \Leftrightarrow ax + by - a - 3b = 0\;\left( {\rm{d}} \right)\).
Vì \(d\left( {I,\left( d \right)} \right) = R\)\( \Leftrightarrow \frac{{\left| {a.3 + b.\left( { - 1} \right) - a - 3b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = 2\)\( \Leftrightarrow \left| {2a - 4b} \right| = 2\sqrt {{a^2} + {b^2}} \)\( \Leftrightarrow \left| {a - 2b} \right| = \sqrt {{a^2} + {b^2}} \)
\( \Leftrightarrow \left( {{a^2} - 4ab + 4{b^2}} \right) = {a^2} + {b^2}\)\( \Leftrightarrow - 4ab + 3{b^2} = 0\)\( \Leftrightarrow b\left( {3b - 4a} \right) = 0\)\( \Leftrightarrow \left[ \begin{array}{l}b = 0\\a = \frac{3}{4}b\end{array} \right.\).
TH1: \(b = 0\) chọn \(a = 1\). Suy ra phương trình tiếp tuyến cần tìm là \(x - 1 = 0\).
TH2: Chọn \(b = 4 \Rightarrow a = 3\). Suy ra phương trình tiếp tuyến cần tìm là \(3x + 4y - 15 = 0\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(x + 2 = \sqrt {x - 1} \).
B. \(x - 1 = \sqrt {x - 3} \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\overrightarrow {{u_1}} = \left( {3;1} \right)\).
B. \(\overrightarrow {{u_2}} = \left( { - 5;4} \right)\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập